
通过培养学生的动手能力发展学生的感性认识与理性认识,培养学生独立思考的习惯.
教材解读
本节内容是在学习了不等式的解集之后的知识内容,在此基础上提出若某数同时满足几个不等式时,如何去确定这个数的取值范围,这就是不等式组的公共解集的确定,在实际生活中同样会遇到一个数所能满足的条件不止一个的问题,这就要用到不等式去确定其解.
学情分析
不等式的解集已经在前一节中学习并运用其解决实际问题,若由多个不等式构成的不等式组的解集如何确定呢?不等式的解集可类比方程的解进行求解,是否不等式组的解与方程组的解也类似呢?因此学生就会进行类比,进而可得出其解集的公共部分.
通过由一元一次不等式,一元一次不等式的解集、解不等式的概念来类推学习一元一次不等式组,一元一次不等式组的解集,解不等式组这些概念,发展学生的类比推理能力.
2.通过确定不等式组的解集与确定方程组的解集进行比较,抽象出这二者中的异同,由此理解不等式组的公共解集.
1.通过由学生动手操作:用各种不同长度的木棒去拼三角形,归纳出能拼出三角形的各边长之间的关系和不能拼成三角形的三边的特征,目的是归纳出同时符合几不同条件的不等式的公共范围,即不等式组的解集.毛
(三)探究拓展
6.已知不等式组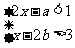 的解集为-1<x<1,则(a+1)(b-1)的值等于多少?
的解集为-1<x<1,则(a+1)(b-1)的值等于多少?
(二)创新提升
5.是否存在实数x,使得x+3<5,且x+2>4.
(一)双基练习
1.解不等式组: 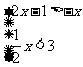
2.解不等式组: 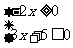
3.解不等式组: 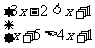
4.解不等式组: 
(三)归纳总结,知识回顾
1.你是如何确定方程组的解的?
方程组的解即是指同时满足各个方程的解.
2.方程组的解与不等式组的解有什么异同?
无论是方程组还是不等式组,它们的解均是指同时满足各个方程(不等式)的解的公共部分,但方程组的解一般只有一组,而不等式组的解一般有很多范围可选择.
3.不等式组的解的四种情形.
作业设计
(二)导入知识,解释疑难
1.教材内容讲解
通过以上分析可知一般地,几个不等式的解集的公共部分,叫做由它们所组成的不等式组的解集,解不等式组就是求它的解集.
例:解下列不等式组,并把解集在数轴上表示出来.
(1) 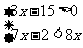 (2)
(2)
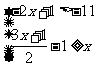
(3) 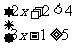 (4)
(4)
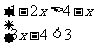
解:(1)由①得x>5,由②得x>-2,在数轴上表示为如图.
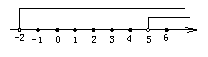
它们的公共部分为x>5,故不等式组的解集为x>5.
(2)由不等式①得x<6,由不等式②得x≥1,在数轴上表示为如图.
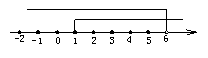
它们的公共部分为1≤x<6,即为不等式组的解集.
(3)由不等式①得x<1,由不等式②得x≥2,在数轴上表示为如图.
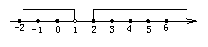
它们没有公共部分,故此不等式组无解.
(4)由不等式①得x<-3,由不等式②得x<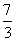 ,在数轴上表示为如图.
,在数轴上表示为如图.
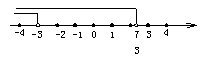
它们的公共部分是x<-3,即为不等式组的解集.
由上述四例可发现不等式组的解集有四种情况:
若a>b:①当 时,则不等式的公共解集为x>a;
时,则不等式的公共解集为x>a;
②当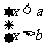 时,不等式的公共解集为b<x<a;
时,不等式的公共解集为b<x<a;
③当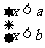 时,不等式的公共解集为x<b;
时,不等式的公共解集为x<b;
④当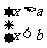 时,不等式组无解.
时,不等式组无解.
练习:解下列不等式组:
(1)  (2)
(2) 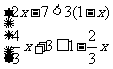 (3)
(3) 
解:(1)不等式2x+5≤3(x+2)的解为x≥-1,不等式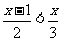 的解为x<3,故不等式组的解集为-1≤x<3.
的解为x<3,故不等式组的解集为-1≤x<3.
(2)不等式2x-7<3(1-x)的解为x<2,不等式 的解为x≤-1,故不等式组的公共解集为x≤-1.
的解为x≤-1,故不等式组的公共解集为x≤-1.
(3)不等式5x+3>8x-2的解为x<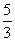 ,不等式
,不等式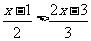 的解为x<3,故不等式组的公共解集为x<
的解为x<3,故不等式组的公共解集为x<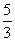 .
.
2.探究活动
试确定以下不等式组的解集:
(1)求不等式组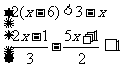 的整数解.
的整数解.
(2)解不等式组 (3)
(3) 
解:(1)2(x-6)<3-x的解集为x<5, 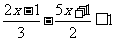 的解集为x≥-1.不等式组的公共解集为-1≤x<5,其整数解有-1,0,1,2,3,4,故不等式组的整数解为-1,0,1,2,3,4.
的解集为x≥-1.不等式组的公共解集为-1≤x<5,其整数解有-1,0,1,2,3,4,故不等式组的整数解为-1,0,1,2,3,4.
(2)不等式2x-5<3x+4的解集为x>-9,不等式4(3x-1)<5(2x+1)的解集为x<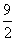 ,不等式
,不等式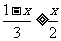 的解集为x≤
的解集为x≤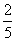 ,不等式组的公共解集必须同时满足这三个不等式,故其解集为-9<x≤
,不等式组的公共解集必须同时满足这三个不等式,故其解集为-9<x≤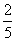 .
.
(3)x-7<0的解集为x<7,x-5<0的解集为x<5,x+3>0的解集为x>-3,x+1>0的解集为x>-1,不等式组的解集必须同时满足这四个不等式,故其公共解集为-1<x<5.
(一)提出问题,引发讨论
在学习不等式组之前,我们来开展小组活动吧,每个小组的同学准备五根小木棒,使它们的长度依次为3cm、10cm、6cm、9cm和14cm,用这些小木棒来搭三角形,要求所搭成的三角形的三边中必须有3cm和10cm这两根木棒,请大家先想想我们还有多少种不同的搭配方式,它们都能搭出三角形吗?再动手试试,验证你们的想法.
搭配方式有三种:3cm、10cm、6cm;3cm、10cm、9cm;3cm、10cm、14cm.但并不是每种搭配方式都能搭成三角形.要构成三角形,必须有两条较短的边拼起来后要略比长边长,也即“任意两边之和大于第三边”,将此不等式变形后成为“任意两边之差小于第三边”,这样可发现只有一种搭配方式可构成三角形,通过拼图验证可得到如课本P143中图.

用不等式来解释,设第三边长为xcm,则有x>10-3又x<10+3,即x>7与x<13,这二者并不矛盾,比7大比13小的数在数轴上可表示为如图9.3-1-1的阴影部分,在这部分数中任取一个都能与10cm和3cm构成一个三角形,所给的三条边6cm、9cm、14cm中只有9cm符合要求.这就是说第三边的取值必须同时满足两个条件:比7大且比13小,把x>7与x<13组合成一个整体即构成一元一次不等式组,即把两个不等式合起来,组成一个一元一次不等式组.由此例可知不等式组的解集即为各个不等式的解集的公共部分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com