4．不等式组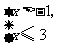的解集为_____，这个不等式组的整数解是_____．

3．解不等式组解不等式得_____，解不等式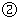得_____，所以不等式组的解集是_____．

2．不等式组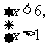的解集是_____；不等式组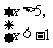的解集是_____．

1．不等式组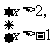的解集是_____；不等式组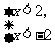的解集是_____．

3．求同时满足不等式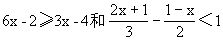的整数解．

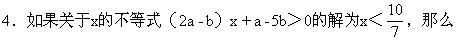
关于x的不等式ax＞b的解是什么？

2．解下列关于x的不等式或不等式组：

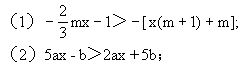
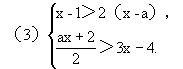
1．解下列不等式或不等式组：

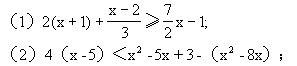
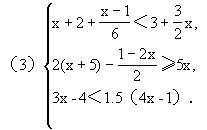
3．一次不等式的一般解法

　一元一次不等式像方程一样，经过移项、合并同类项、整理后，总可以写成下面的标准型：ax＞b，或ax＜b．为确定起见，下面仅讨论前一种形式．

　 一元一次不等式ax＞b．

　 (3)当a=0时，

用区间表示为(-∞，+∞)．

　例1 解不等式

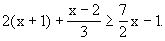
　解 两边同时乘以6得

12(x+1)+2(x-2)≥21x-6，

化简得

-7x≥-14，

　两边同除以-7，有x≤2．所以不等式的解为x≤2，用区间表示为(-∞，2]．

　例2 求不等式

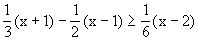
　的正整数解．

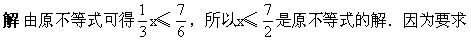
正整数解，所以原不等式的正整数解为x=1，2，3．

　例3 解不等式

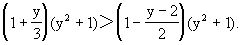
　分析与解 因y2+1＞0，所以根据不等式的基本性质有

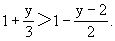
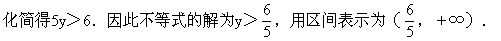
　例4 解不等式

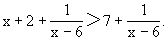
　为x+2＞7，解为x＞5．这种错误没有考虑到使原不等式有意义的条件：x≠6．

　解 将原不等式变形为

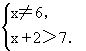
　解之得

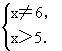
　所以原不等式的解为x＞5且x≠6．

　例5 已知2(x-2)-3(4x-1)=9(1-x)，且y＜x+9，试比较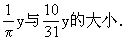

　解 首先解关于x的方程得x=-10．将x=-10代入不等式得

y＜-10+9，即y＜-1．

　例6 解关于x的不等式：

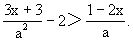
　解 显然a≠0，将原不等式变形为

3x+3-2a²＞a-2ax，

　即

(3+2a)x＞(2a+3)(a-1)．

　说明 对含有字母系数的不等式的解，也要分情况讨论．

　例7 已知a，b为实数，若不等式

(2a-b)x+3a-4b＜0

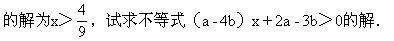
　解 由(2a-b)x+3a-4b＜0得

(2a-b)x＜4b-3a．

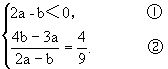
　由②可求得

　将③代入①得

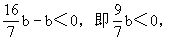
　所以b＜0．于是不等式(a-4b)x+2a-3b＞0可变形为

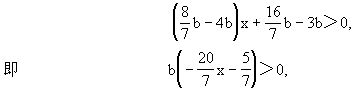
　因为b＜0，所以

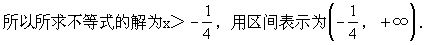
　下面举例说明不等式组的解法．

　不等式组的解是不等式组中所有不等式解的公共部分．

　若不等式组由两个不等式组成，分别解出每一个不等式，其解总可以归纳成以下四种情况之一(不妨设α＜β)：

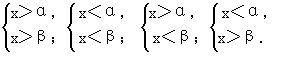
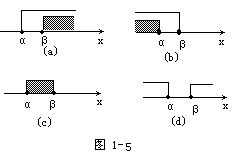
　解分别为：x＞β；x＜α；α＜x＜β；无解．如图1－5(a)，(b)，(c)，(d)所示．

　若不等式组由两个以上不等式组成，其解可由下面两种方法求得：

　(1)转化为求两两不等式解的公共部分．如求解

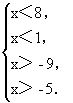
　(2)不等式组的解一般是个区间，求解的关键是确定区间的上界与下界，如求解

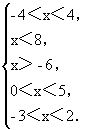
　确定上界：由x＜4，x＜8，x＜5，x＜2，从4，8，5，2这四个数中选最小的数作为上界，即x＜2．

　确定下界：由x＞-4，x＞-6，x＞0，x＞-3．从-4，-6，0，-3中选最大的数作为下界，即x＞0．

　确定好上、下界后，则原不等式组的解为：0＜x＜2．不等式组中不等式的个数越多，(2)越有优越性．

　例8 解不等式组

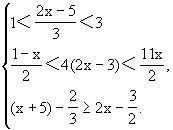
　解 原不等式组可化为

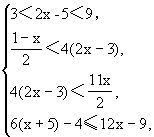
　解之得

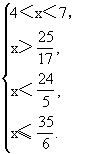
　例9 解关于x的不等式组

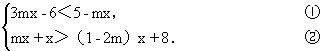
　解 解①得

4mx＜11，③

　　 解②得 　　　　　　　3mx＞8． ④

　(1)当m=0时，③，④变为

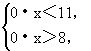
原不等式组无解．

　(2)当m＞0时，③，④变形为

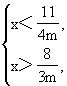
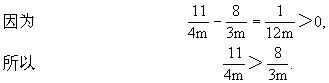
　(3)当m＜0时，由③，④得

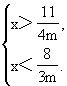
练习六

2．区间概念

　在许多情况下，可以用不等式表示数集和点集．如果设a，b为实数，且a＜b，那么

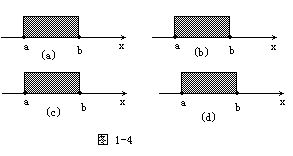
　(1)满足不等式a＜x＜b的数x的全体叫作一个开区间，记作(a，b)．如图1－4(a)．

　(2)满足不等式a≤x≤b的数x的全体叫作一个闭区间，记作[a，b]．如图1－4(b)．

　(3)满足不等式a＜x≤b(或a≤x＜b)的x的全体叫作一个半开半闭区间，记作(a，b](或[a，b))．如图1－4(c)，(d)．

1．不等式的基本性质

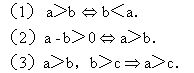
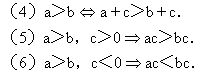
　这里特别要强调的是在用一个不等于零的数或式子去乘(或去除)不等式时，一定要注意它与等式的类似性质上的差异，即当所乘(或除)的数或式子大于零时，不等号方向不变(性质(5))；当所乘(或除)的数或式子小于零时，不等号方向要改变(性质(6))．