9. 若(x+m)(x+n)=x²-6x+5，则(　 )

　　 A．m，n同时为负；　　 B．m，n同时为正；

　 C．m，n异号；　　　　 D．m，n异号且绝对值小的为正.

8. 下列计算正确的是

A.a³·(－a²)= a⁵； B.(－ax²)³=－ax⁶；

C.3x³－x(3x²－x+1)=x²－x；　　　　　　　　 D.(x+1)(x－3)=x²+x－3.

7.下列多项式相乘的结果是a²-a-6的是(　 )

　 A．(a-2)(a+3)；　　 B．(a+2)(a-3)；　 C．(a-6)(a+1)；　　 D．(a+6)(a-1).

6.下列说法不正确的是(　 )

A．两个单项式的积仍是单项式；　　

B．两个单项式的积的次数等于它们的次数之和；

　　 C．单项式乘以多项式，积的项数与多项式项数相同；

　 D．多项式乘以多项式，合并同类项前，积的项数等于两个多项式的项数之和.

5.当a=-1时，代数式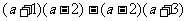的值等于　　　　　　　　　　　 .

4.若(x-8)(x+5)=x²+bx+c，则b=____ __，c=____　 ___．

3.计算：(x+1)(x²-x+1)=____　 _　　 ____．

2.计算：(3-2x)(2x-2)=___　 ___．

1.计算(5b+2)(2b-1)=______　 _.

解不等式(2)，得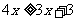

∴原不等式无解

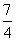14，解方程5x-2m=3x-6m+1得x=．要使方程的解在-3与4之间，只需-3<<4．解得-<m<．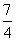

15，设至少同时开放n个检票口，且每分钟旅客进站x人，检票口检票y人．依题意，得第一、二两个式子相减，得y=2x．把y=2x代入第一个式得a=30x．把y=2x，a=30x代入③得n≥3.5．∵n只能取整数，∴n=4，5，…答：至少要同时开放4个检票口．

16，解：(1)根据题意，最少花费为：6×5+5×10+4×15=140元．(2)设三等奖的奖品单价为x元，根据题意得解得4≤x≤6，因此有3种方案分别是：方案1：三等奖奖品单价6元，二等奖奖品单价24元，一等奖奖品单价120元．方案2：三等奖奖品单价5元，二等奖奖品单价20元，一等奖奖品单价100元．而表格中无此奖品故这种方案不存在，舍去．方案3：三等奖奖品单价4元，二等奖奖品单价16元，一等奖奖品单价为80元．方案1花费：120×5+24×10+6×15=930元，方案2花费：80×5+16×10+4×15=620元，其中花费最多的一种方案为一等奖奖品单价120元，二等奖奖品单价24元，三等奖奖品单价6元，共花费奖金930元．点拨：(1)学校买奖品花钱最少，则奖品依次为相册，笔记本，钢笔等这些单价偏低的商品分别作为一，二，三等奖品．(2)根据题目中包含的不等关系，建立不等式组，再由奖品单价为整数，求出符合题意的整数解．确定购买方案．

17，解：(1)设A队胜x场，平y场，负z场，则用x表示y，z解得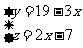：∵x≥0，y≥0，z≥0且x，y，z均为正整数，∴ 解之得3≤x≤6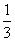，∴x=4，5，6，即A队胜，平，负有3种情况，分别是A队胜4场平7场负1场，A队胜5场平4场负3场，A队胜6场平1场负5场，(2)在(1)条件下，A队胜4场平7场负1场奖金为：(1500+500)×4+(700+500)×4+500×3=16300元，A队胜6场平1场负5场奖金为(1500+500)×6+(700+500)×1+500×5=15700元，故A队胜4场时，该名队员所获奖金最多．点拨：在由已知设胜x场，平y场，负z场，首先根据比赛总场次12场，得分19分，建立方程组，用x表示y，z最后关键在于分析到题目中隐含的x≥0，y≥0，z≥0且x，y，z为整数从而建立不等式组求到x的值．(2)把3种情况下的奖金算出，再比较大小．

备用题：

1，C.

1，解：设有x名学生获奖，则钢笔支数为(3x+8)支，依题意得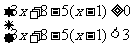解得5<x≤6，∵x为正整数.∴x=6，把x=6代入3x+8=26.答：该校有6名学生获奖，买了26支钢笔．点拨：设出获奖人数，则可表示奖励的钢笔支数，再根据题目中第二个已知条件，每人送5支，最后一人所得支数不足3支，隐含了0≤最后一人所得钢笔支数<3这样的不等式关系列不等式组，求出x的取值范围5<x≤6，又x表示人数应该是正整数，所以x=6，3x+6=26，因此一共有6名学生获奖，买了26支钢笔发奖品．

3，解：设生产甲型玩具x个，则生产乙型玩具(100-x)个，依题意得：解之得：43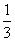≤x≤45，∵x为正整数，∴x=44或45，100-x=56或55，故能实现这个计划，且有2种方案，第1种方案：生产甲型玩具44个，生产乙型玩具56个．第2种方案：生产甲型玩具45个，生产乙型玩具55个．