9.3保险公司怎样才能不亏本　

[教学目标]

　 见作业纸

4、如图,矩形ABCD中,AB=6,AD=8,点P在BC边上移动(不与点B、C重合),设PA=x,点D到PA的距离DE=y.求y与x之间的函数关系式及自变量x的取值范围.

3、某地上年度电价为0.8元­/­度,年用电量为1亿度.本年度计划将电价调至0.55元至0.75元之间.经测算,若电价调至x元,则本年度新增用电量y(亿度)与(x－0.4)(元)成反比例,当x=0.65时,y=-0.8.

(1)求y与x之间的函数关系式；

(2)若每度电的成本价为0.3元,则电价调至多少元时,本年度电力部门的收益将比上年度增加20%? [收益=(实际电价－成本价)×(用电量)]

2、一定质量的氧气,它的密度ρ (kg/m³)是它的体积V( m³) 的反比例函数, 当V=10m³时,ρ=1.43kg/m³. (1)求ρ与V的函数关系式；(2)求当V=2m³时求氧气的密度ρ.

1、见P92练习

例1、小明将一篇24000字的社会调查报告录入电脑，打印成文.

(1)如果小明以每分种120字的速度录入，他需要多少时间才能完成录入任务？

(2)录入文字的速度v(字/min)与完成录入的时间t(min)有怎样的函数关系？

(3)小明希望能在3h内完成录入任务，那么他每分钟至少应录入多少个字？

例2某自来水公司计划新建一个容积为的长方形蓄水池.

(1)　　　 蓄水池的底部S与其深度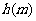有怎样的函数关系？

(2)　　　 如果蓄水池的深度设计为5m，那么蓄水池的底面积应为多少平方米？

(3)　　　 由于绿化以及辅助用地的需要，经过实地测量，蓄水池的长与宽最多只能设计为100m和60m，那么蓄水池的深度至少达到多少才能满足要求？(保留两位小数)

为了预防“非典”,某学校对教室采用药熏消毒法进行消毒, 已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:

(1)药物燃烧时,y关于x 的函数关系式为: ________, 自变量x 的取值范围是:_______,药物燃烧后y关于x的函数关系式为_______.

(2)研究表明,当空气中每立方米的含药量低于1.6mg时学生方可进教室,那么从消毒开始,至少需要经过______分钟后,学生才能回到教室;

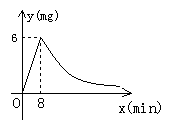(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?