
2.通过图形面积的计算,感受乘法公式的直观解释,了解公式的几何背景.
1.会推导完全平方公式、平方差公式,并能正确运用公式进行简单计算.
2.作业:课本70页:第1、2、3题
教学素材:
A组题:
(1).2x2y.3xy2
(2) .4a2x5.(-3a3bx)
(3).5an+1b.(-2a)
(4).(a2c)2.6ab(c2)3
B组题:
(1).5an+1b.(-2a)
(2).(a2c)2.6ab(c2)3
1. 小结:(1)单项式乘单项式法则;
(2)运用时应注意什么?
3. 巩固练习
(1).2x2y.3xy2
(2) .4a2x5.(-3a3bx)
课本69页--70页:第1、2题
小结与作业
2.例题
计算:(1)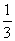 a
a ·(6ab);
·(6ab);
(2)(2x) ·(-3xy
·(-3xy ).
).
解: (1)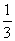 a
a ·(6ab)
·(6ab)
= (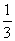 ×6)·(a
×6)·(a ·a)·b
·a)·b
=
2a b;(教师规范格式)
b;(教师规范格式)
(2)(2x) ·(-3xy
·(-3xy ).
).
= 8x ·(-3xy
·(-3xy )
)
= [8×(-3)](x ·x)y
·x)y
= -24x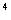 y
y .
.
小结:这节课你有何收获?


我们可以看到,“电视墙”是一个长方形,由9个小长方形组成。
从整体上看,“电视墙”的面积为长方形的长与宽的积:3a·3b;
从局部看,“电视墙”中的每个小长方形的面积都是ab,“电视墙”的面积是这些小长方形的面积和:9ab。
于是,我们有:3a·3b = 9ab.
新课讲解:
1.探索研究
一起来观察上面这个等式:3a·3b = 9ab,根据上学期的学习,同学们知道,3a、3b都是单项式,9ab也是个单项式,那么计算时是否有一定的规律性?4ab ·5b这两个单项式的积是20ab
·5b这两个单项式的积是20ab 吗?
吗?
请学生回答,教师加以总结归纳:
两个单项式3a与3b相乘,只要把两个单项式的系数3与3相乘,再把这两个单项式的字母a与b相乘,即3a·3b =(3×3)·(a·b)= 9ab.
4ab ·5b这两个单项式的积是20ab
·5b这两个单项式的积是20ab 。
。
同学们回答的太棒了,两个单项式相乘,实际上是运用了乘法交换律与结合律。由此,我们可以得到单项式乘单项式法则: 单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里含有的字母,则连同它们的指数作为积的一个因式。
16.根据以下10个乘积,回答问题:
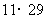




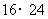
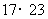



(1)试将以上各乘积分别写成一个“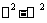 ”(两数平方差)的形式,并将以上10个乘积按照从小到大的顺序排列起来;
”(两数平方差)的形式,并将以上10个乘积按照从小到大的顺序排列起来;
(2)若乘积的两个因数分别用字母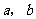 表示(
表示(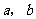 为正数),请观察给出
为正数),请观察给出 与
与 的关系式.(不要求证明)
的关系式.(不要求证明)
(3)若用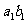 ,
, ,
, ,
,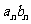 表示
表示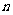 个乘积,其中
个乘积,其中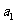 ,
, ,
,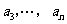 ,
,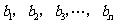 为正数.请根据(1)中乘积的大小顺序猜测出一个一般结论.(不要求证明)
为正数.请根据(1)中乘积的大小顺序猜测出一个一般结论.(不要求证明)
15.设m,n为自然数,且满足: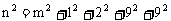 ,求m,n的值.
,求m,n的值.
14. 将4个数 排成2行、2列,两边各加一条竖直线记成
排成2行、2列,两边各加一条竖直线记成 ,定义
,定义
 ,上述记号就叫做2阶行列式.若
,上述记号就叫做2阶行列式.若
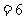 ,则
,则  .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com