
1、把下列各式分解因式
(1)16a4+24a2b2+9b4 (2)(x+y)2-10(x+y)+25
3. 分解因式(板演)
(1)a2-4a+4 (2)a2-12ab+36b2 (3)25x2+10xy+y2
探索活动二:公式中的a、b可表示什么?学生讨论易知a、b可以为任意的数、字母或多项式.
如:a2-4a+4
↓把a换成(m+n)
(m+n)2-4(m+n)+4 怎么分解呢?请看例2
例2把下列各式分解因式
(1)16a4+8a2+1 (2)(m+n)2-4(m+n)+4
分析:许多情况下,不一定能直接使用公式,需要经过适当的组合,变形成公式的形式.
解:(1)16a4+8a2+1 (2) (m+n)2-4(m+n)+4
=(4a2)2+2×4a2+1 =(m+n)2-2×2(m+n)+22
=(4a2+1)2 =[(m+n)-2]2=(m+n-2)2
变式训练 若把16a4+8a2+1变形为16a4-8a2+1会怎么样呢?学生讨论作答
16a4-8a2+1
=(4a2)2-2×4a2+1
=(4a2-1)2 (这里4a2-1可继续分解)
=[(2a+1)(2a-1)]2=(2a+1)2(2a-1)2
例3 (1)简便计算20042-4008×2005+20052
(2)已知a2-2a+b2+4b+5=0,求(a+b)2005的值.
解:(1) 20042-4008×2005+20052=20042-2×2004×2005+20052=(2004-2005)2=1
(2) a2-2a+b2+4b+5=0变形为
(a-1)2+(b+2)2=0 ∴a-1=0,b+2=0 ∴a=1,b=-2
(a+b)2005=[1+(-2)]2005=-1
说明 用完全平方公式解决两道有用的实际问题使学生享受到运用所学知识的乐趣和心理满足,激励他们的求知欲望.
练一练:
2. 分解因式:-a2+2ab-b2=
分解因式:-a2-2ab-b2=
例1 把下列各式分解因式
(1)x2+10x+25 (2)4a2+36ab+81b2
分析 重点是指出什么相当于公式中的a、b,并适当的改写为公式的形式,
解:(1)x2+10x+25 (2) 4a2+36ab+81b2
=x2+2×x×5+52 =(2a)2-2×2a×9b+(9b)2
=(x+5)2 =(2a-9b)2
说明 本题是基础题,使学生体会用完全平方公式如何分解因式,以及解题格式,学生尝试去做,教师在对不同意见作比较,评价、培养学生的解题能力.
练一练(及时训练,巩固新知)
1. 下列能直接用完全平方公式分解的是( )
A.x2+2xy-y2 B.-x2+2xy+y2 C.x2+xy+y2 D.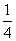 x2-xy+y2
x2-xy+y2
把乘法公式(a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2
反过来,就得到a2+2ab+b2=(a+b)2 a2-2ab+b2=(a-b)2
提出问题 自主探索:
问题1 两公式左边是几项式?三项式,再考虑一下平方差公式.左边是几项式与之比较.
问题2 这三项式有什么特点?其中两项同号,且能写成两数的平方和的形式,另一项是这两数乘积的2倍,它的符号可正可负,口决:“首平方尾平方,二数乘积在中央”有了平方差公式的经验学生自已不难得出,教师重在引导,不要替学生解答好,学法上可采取小组讨论,全班交流.
问题3 若用△代表a,○代表b,两式是什么形式?△2+2△×○+○2=(△+○)2,△2-2△×○+○2=(△-○)2
说明 经过观察、比较、思考、类比,培养了学生的思维能力,这里学生自己观察、自主探索出公式的本质特征,轻松地掌握本节的重点,同时化解了难点.
问题4 将a2-4a-4符合吗?为什么?
问题5 a2+6a+9符合吗? 相当于a, 相当于b.
a2+6a+9=a2+2×( )×( )+( )2=( )2
a2-6a+9=a2-2×( )×( )+( )2=( )2
(六)作业
1.课本P95习题9.6第一题.
2.课本P95习题9.6第二题.
3.课本P95习题9.6第六题的第一题
选做
利用因式分解计算:
(1)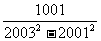
(2)(1-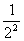 )(1-
)(1-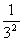 )(1-
)(1- )…(1-
)…(1-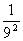 )(1-
)(1-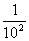 )
)
(3)已知:4m+n=90,2m-3n=10,求(m+2n)2-(3m-n)2的值.
(五)小结
学生自己说出通过本节课的学习进一步理解了整式的乘法与因式分解的关系.能用自己的语言说出平方差公式的特点.能体会出公式中的字母a、b不仅可以表示数字,而且可以是单项式、多项式.
(四)练习
1.下列分解因式是否正确:
(1)-x2-y2=(x+y)(x-y)
(2)9-25a2=(3+25a)(3+25b)
(3)-4a2+9b2=(-2a+3b)(-2a-3b)
2.把下列各式分解因式:
(1) 36-x2 (2) a2-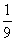 b2 (3) x2-16y2
b2 (3) x2-16y2
(4) x2y2-z2 (5) (x+2)2-9 (6)(x+a)2-(y+b)2
(7) 25(a+b)2-4(a-b)2 (8) 0.25(x+y)2-0.81(x-y)2
3.在边长为16.4cm的正方形纸片的四角各剪去一边长为1.8cm的正方形,求余下的纸片的面积.
4.已知x2-y2=-1 , x+y=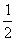 ,求x-y的值.
,求x-y的值.
(三)例题教学
例1 把下列多项式分解因式:
(1) 36-25x2 (2) 16a2-9b2
分析:观察是否符合平方差公式的形式,应引导学生把36、25x2、16a2、9b2改写成62、(5x)2、(4a)2和(3b)2形式,能否准确的改写是本题的关键.
解: 36-25x2=62-(5x)2
=(6+5x)(6-5x)
16a2-9b2=(4a)2-(3b)2
=(4a+3b)(4a-3b)
说明: (1)对于多项式中的两部分不是明显的平方形式,应先变形为平方形式,再运用公式分解,以免出现16a2-9b2=(16a+9b)(16a-9b)的错误.
(2)在此还要提醒防止出现分解后又乘开的现象,这是旧知识的“倒摄作用”所引起的现象.
例2 如图,求圆环形绿化区的面积.
解: 352π-152π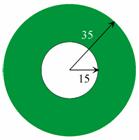
=π(352-152)
=(35+15)(35-15)π
=50×20π
=1000π(m2)
这个绿化区的面积是1000πm2
说明:在这里列出算式后可以让学生自己讨论怎么计算,要让学生解释他的解法,可能解释为逆运用乘法结合律,也可能解释为合并同类项,都要予以肯定,在这儿不要怕浪费时间,通过比较得出上述解法和前一节的提取公因式是一致的,从而为分解因式的一般步骤打下伏笔,即:先提公因式,再运用公式.
例3 把下列多项式分解因式:
1. (x+p)2-(x+q)2 2. 9(a+b)2-4(a-b)2
分析:在这里,尤其要重视对运用平方差公式前的多项式观察和心算,而后是进行变形.这一点在这儿尤为重要.
解: (x+p)2-(x+q)2
=[(x+p)+(x+q)][(x+p)-(x+q)]
=(2x+p+q)(p-q)
9(a+b)2-4(a-b)2
=[3(a+b)]2-[2(a-b)]2
=[3(a+b)+2(a-b)] [3(a+b)-2(a-b)]
=(5a+b)(a+5b)
说明:设计本题的目的是让学生加深平方差公式中的a、b不仅可以表示数字、单项式,也可以是多项式,进一步渗透整体、换元的思想.
例4.(供选择)观察下列算式回答问题:
32-1=8
52-1=24=8×3
72-1=48=8×6
92-1=80=8×10
………
问:根据上述的式子,你发现了什么?你能用自己的语言表达你所发现的结论吗?你能用数学式子来说明你的结论是正确的吗?
解: 任意一个奇数的平方与1的差是8的整数倍.
(2n+1)2-1 =[(2n+1)+1][(2n+1)-1]
= (2n+2)·2n
=2(n+1)·2n
=4n(n+1)
因为n是整数,所以n、n+1是两个连续的整数,而两个连续的整数一定有一个是偶数,即n(n+1)是2的倍数,因此4n(n+1)是8的倍数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com