
2.例题:
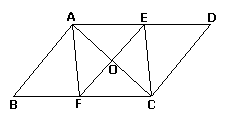 例1:已知:平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F,求证:四边形AFCE是菱形。
例1:已知:平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别交于E、F,求证:四边形AFCE是菱形。
解题指导:(1)有一组邻边相等的平行四边形;(差)
(2)四条边都相等的四边形;(良)
(3)对角线互相垂直的平行四边形;(优)
1.菱形的识别方法:
①菱形是有一组邻边相等的平行四边形,因此在识别一个四边形是不是菱形时,首先看这个四边形是不是平行四边形,再看它两邻边是不是相等,这种用“定义”识别我们已经知道是最重要和最基本的识别方法。今天我们研究菱形有几种识别方法。
总结出识别方法1:
有一组邻边相等的平行四边形是菱形。
②大家都知道,菱形的特别之处在于它的邻边相等,能否从边的特点来识别菱形呢?
学生猜想:会从平行四边形、矩形的识别方法和特征联想到。给出:
问题1:有四边相等的四边形是菱形吗? …(投影)
分析问题1:因为四边形的四边都相等,因此一定有一组邻边相等,只要再证出它是平行四边形就可由定义证明此问题是肯定的。(由学生自己证明书写过程)。
总结出识别方法2:
四边相等的四边形是菱形。
③我们再考虑菱形的其他特殊的特征,如从对角线的角度来考虑,那么,是否可以从对角线上来识别菱形呢?给出:
问题2:对角线互相垂直的平行四边形是菱形吗?…(投影)
分析问题2:因为平行四边形是条件,所以只需证有一组邻边相等即可。为加深学生对问题2条件的理解,可举反例:如:两条对角线相等的四边形,是不是菱形?两条对角线相等且互相平分的四边形是不是菱形?两条对角线互相垂直平分的四边形是不是菱形?(学生可自行画图观察,进行证明过程的书写训练)
可知,由对角线垂直推不出四边形是平行四边形,巩固学生对识别方法3的印象和理解。
总结出识别方法3:
对角线互相垂直的平行四边形是菱形。
1、复习菱形的有关概念及边、角、对角线方面的特征。
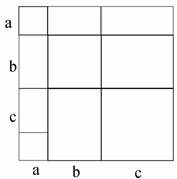
3. 利用图形面积因式分解
①a2+3ab+2b2

②a2+b2+c2+2ab+2bc+2ac
2. 已知x+y=4 xy=2 求2x3y+4x2y2+2xy3的值
必做:课本P95习题9.6 5、6
选做:
1. 分解因式
(1)80a2(a+b)-45b2(a+b) (2)(x2-2xy)+2y2(x2-2xy)+y4
(3)(x+y)2-4(x2-y2)+4(x-y)2
学生通过例题的学习及练习自己总结在综合运用提公因式法和运用公式法分解因式时要注意的问题和解题步骤,可由1个或几个学生回答,互相补充,教师归纳(投影)
(1)如果多项式各项有公因式,应先提公因式,再进一步分解.
(2)分解因式必须分解到每个多项式的因式都不能再分解为止.
(3)因式分解的结果必须是几个整式的积的形式.
即:“一提”、“二套”、“三查”特别强调“三查”,检查多项式的每一个因式是否还能继续分解因式,还可以用整式乘法检查因式分解的结果是否正确.
(四)练习
1、辨析 分解因式 a4-8a2+16
a4-8a2+16=(a2-4)2=(a+2)2(a-2)2=(a2+2a+4)(a2-2a+4)
这种解法对吗?如果不对,指出错误原因.
说明:本题考查学生因式分解与整式乘法的意义,错因是混淆了二者的区别,走了“回头路”
2. 选择题:
多项式①16x5-x ②(x-1)2-4(x-1)+4 ③(x+1)4-4x(x+1)2+4x2 ④-4x2-1+4x分解因式后,结果含有相同因式的是( )
A、①② B、③④ C、①④ D、②③
3. 填空:
请写出一个三项式,使它能先提公因式,再运用公式法来分解因式,你编的三项式是 ,分解因式的结果是 .
本题设计说明:学生不仅要学会课本上的例题和习题,而且要懂得借助课本内容的思想方法去编拟习题,这是创新教育的一种表现形式.
4. 把下列各式分解因式
(1)3ax2-3ay4 (2)-2xy-x2-y2 (3)3ax2+6axy+3ay2
(4)x4-81 (5)(x2-2y)2-(1-2y)2
(6)x4-2x2+1 (7)x4-8x2y2+16y4
分两组板演:(1)~(3)一组,(4)~(7)为另一组,也可以投影部分学生的解答过程进行点评.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com