
7.在密度的计算公式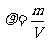 中,当物体的m一定时,密度
中,当物体的m一定时,密度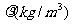 与体积V(m3)之间的函数图像可表示为下图的( )
与体积V(m3)之间的函数图像可表示为下图的( )
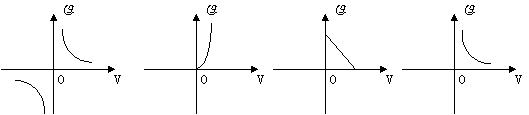

A B C D
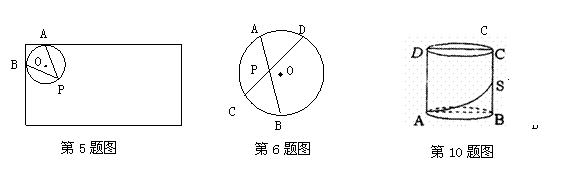
6.如图⊙O中弦AB、CD相交于点P,PC=PD,PA=3cm,PB=4cm,则CD长为( )
 A.4
A.4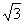 B.4cm C.2
B.4cm C.2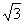 cm D.2cm
cm D.2cm
5.如图,将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙的切点为A、B,点P是桌子边缘上一点,则∠APB等于( )
A.30° B.45° C.60° D.不能确定
4.只用一种正多边形进行平面镶嵌,这种正多边形不能是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
3.截至2005年一季度末,江苏省企业养老保险参保人数达850万,则参保人数用科学记数法表示为( )
A.8.50×106人 B.8.50×105人 C.0.850×106人 D.8.50×107人
2.下列计算中,不正确的是( )
A.3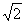 +2
+2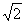 =5
=5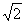 B.
B.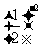 =4 C.(π-3.14)0=1 D.(-x)3·(-x)2=x5
=4 C.(π-3.14)0=1 D.(-x)3·(-x)2=x5
1.函数y=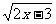 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A.x≠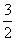 B.x>
B.x>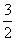 C.x≥
C.x≥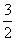 D.x<
D.x<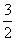
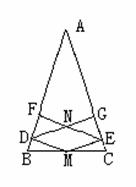
(1)已知:如图,M是等腰三角形ABC底边
BC上的中点,DM⊥AB,EF⊥AB ME⊥AC,
DG⊥AC。求证:四边形MEND是菱形。
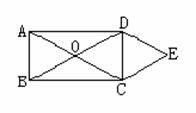
(2)如图,O是矩形ABCD的对角线的交点,
DE∥AC,CE∥BD,DE和CE相交于E,
求证:四边形OCED是菱形。
板书设计:
|
12.2几种特殊的平行四边形(4) 1.菱形特征的几何语言: 2.菱形的识别方法及证明: ………………………… …………………………… ………………………… …………………………… 3.例题: 4.学生练习: ………………………… …………………………… ………………………… …………………………… |
教学后记
经历探索菱形的性质和识别条件的过程,在操作活动和观察,分析过程中发展学生的主动探究习惯和初步审美意识,进一步了解和体会说理的基本方法。
 这堂课的主要内容是对菱形进行识别,可以运用以下几种方法来说明,①有一组邻边相等的平行四边形是菱形………………(定义);②对角线互相垂直的平行四边形是菱形;③四边都相等的四边形是菱形。
这堂课的主要内容是对菱形进行识别,可以运用以下几种方法来说明,①有一组邻边相等的平行四边形是菱形………………(定义);②对角线互相垂直的平行四边形是菱形;③四边都相等的四边形是菱形。
3.练习:[基础训练题]:
(1)菱形可根据哪些进行识别?填写下表、填图:
|
|
应具备的条件 |
|
|
菱形的定义 |
|
|
|
菱形的识别1 |
|
|
|
菱形的识别2 |
|
|
|
菱形的识别3 |
|
|
(2)对角线互相垂直的四边形是菱形。( ) (3)对角线互相平分的四边形是菱形。( )
(4)两组对边分别平行,且对角线 的四边形是菱形。
(5)两组对边分别相等,且对角线互相垂直的四边形是菱形。( )
(6)对角线互相平分的四边形是 。(7)对角线互相垂直平分的四边形是 。
(8)对角线相等且互相平分的四边形是 。
(9)画一个菱形,使它的对角线分别是6cm、8cm 。
(10)在平行四边形ABCD中,AC交BD于O,下列结论中错误的是( )
A:AB=CD,B=D B:AC=BD且互相平分
C:当ACBD时,四边形ABCD是菱形 D:SAOB=SABCD
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com