(二)综合题讲解

1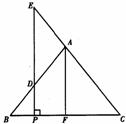．如图，在△ABC中，AB＝AC＝5，BC＝6，F为BC的中点．P是BF上的一点，过点P作BC的垂线交AB于D，交CA的延长线于E．若设 BP＝x，那么，图中有些量(线段、面积等)可以看作x的函数，如，PC＝6－x，PF＝3－x等．除以上两例外，请你再写出一个关于x的函数解析式，并加以证明．(不要添加辅助线和其它字母)

2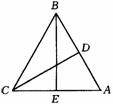．图，在△ABC中，点D、E分别在边AB、AC上．给出5个论断： 　 ① CD⊥AB，② BE⊥AC，③ AE＝CE，④ ∠ABE＝30°，⑤ CD＝BE ⑴ 如果论断①、②、③、④都成立，那么论断⑤一定成立吗？答：　　　　　 　； ⑵ 从论断①、②、③、④中选取3个作为条件，将论断⑤作为结论，组成一个真命题，那么你选的3个论断是　 　　　　　　　　　(只需填论断的序号)； ⑶ 用⑵中你选的3个论断作为条件，论断⑤作为结论，组成一道证明题，画出图形，写出已知、求证：并加以证明。(徐州市)

4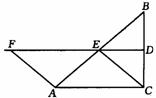．　 如图，在△ABC中，∠ACB＝90°，BC的垂直平分线DE交BC于D，交AB于E，F在DE上，并且AF＝CE． (1)求证：四边形ACEF是平行四边形； (2)当∠B的大小满足什么条件时，四边形ACEF是菱形？请回答并证明你的结论； (3)四边形ACEF有可能是正方形吗？为什么？(海南省)

5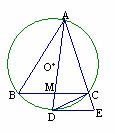．如图,在△ABC中,∠A的平分线AM与BC交于点M,且与△ABC的外接圆O交于点D.过D作⊙O的切线交AC的延长线于E,连结DC, 求证：　　　　　　　　　　　　　　　 .要求：请根据题目所给的条件和图形,在题中的横线上写出一个正确的结论,并加以证明(在写结论和证明时都不能在图中添加其它字母和线段).按证明结论时需要用到的已知条件的多少给分,若用足已知条件而证得结论即可得满分.

(一)填空题(A组同学只做1-7)

1.　　　 请写出你熟悉的两个无理数__________.

2.　　　 如图，如果横行上的两个数字之和相等，竖列上的两个数字之和相等，那么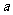、、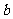、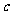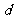依次可为　　　 .(只需填写一组你认为合适的数字即可)

3.　　　 如图，D、E两点分别在AC、AB上，且DE与BC不平行，请填上一个你认为合适的条件： 　　　　　　　　　　　，使得△ADE∽△ABC.

4.　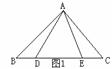　　 写出一个含有字母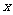的分式(要求：不论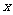取任何实数，该分式都有意义，且分式的值为负)　　　　　　　　　　　 　．

5.　　　 如图1、已知D、E是ΔABC中BC边上的两点，AD=AE，请你再加上一个条件　　　　　　 ，使ΔABE≌ΔACD。

6.　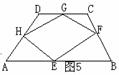　　 如图5、在梯形ABCD中，ADBC，E、F、G、H分别是梯形ABCD各边的中点，当梯形ABCD满条件　　　　　　　 时，四边形EFGH是菱形(填上一个你认为正确的一个条件即可)

7.　　　 如果两个二元一次方程组成的一个二元一次方程组的解是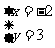，那么写出符合要求的一个二元一次方程组是　　　　　　　　 ；

8.　　　 请你写出函数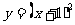与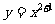具有的一个共同性质　　　　

9.　　　 关于x的一元二次方程x²－x+a(1－a)=O有两个不相等的正根，则a可取值为　　　　　 ．(注：只要填写一个可能的数值即可．)

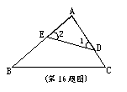
10.　　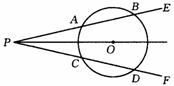 如图，点O是∠EPF的平分线上一点，⊙O和∠EPF的两边分别交于点A、B和C、D，根据上述条件，可以推出　　　　 　　．(要求：填写一个你认为正确的结论即可，不再标注其他字母，不写推理过程)

11.　　 在四边形ABCD中，已知AB∥CD，请补充条件__________________(写一个即可)，使得四边形ABCD为平行四边形；若四边形ABCD是平行四边形，请补充条件________________________(写一个即可)，使得四边形ABCD为菱形。

12.　　 正方形既是轴对称图形又是中心对称图形；反过来，既是轴对称图形又是中心对称图形的图形不一定是正方形．例如，圆既是轴对称图形又是中心对称图形，但圆不是正方形．请你在已学过的几何图形中再举两个例子(只要求写出图形名称)：① 　　　　　；②　　　　　　　　　　　　 　；

13.　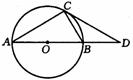　 已知：如图：AB是⊙O的直径，BD＝OB，∠CAB＝30°．请根据已知条件和所给图形，写出三个正确结论(除AO＝OB＝BD 外)；①　　　　 ；②　　　　 ；③　　　　 ．

条件开放型就是要求解题者直接写满足结论的有限个条件，或者根据结论论证应该具备哪些条件；结论开放型就是要求答题者直接写出符合条件的有限个结论，或者根据条件论证出多个结论；策略开放型就是要求答题者从不同角度探索问题，或用不同知识点，或用不同解题路径与方法解决同一个问题。

4．　 综合型：即条件、结论、策略中至少有两项均是开放的；

3．　 策略开放型：即思维策略与解题方法不唯一；

2．　 结论开放型：即在给定的条件下，结论不唯一；

1．　 条件开放型：即问题的条件不完备或满足结论的条件不唯一；

30、(本大题满分11分)如图，在矩形ABCD中，AD＝8，点E是AB边上的一点，AE＝2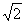，过D、E两点作直线PQ，与BC边所在的直线MN相交点F．

(1)求tan∠ADE的值；

(2)点G是线段AD上的一个动点(不运动至点A、D)，GH⊥DE垂足为H，设DG为x，四边形AEHG的面积为y；请求出y与x之间的函数关系式；

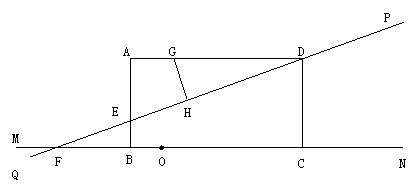(3)如果AE＝2EB，点O是直线MN上的一个动点，以O为圆心作圆，使⊙O与直线PQ相切，同时又与矩形ABCD的某一边相切，问满足条件的⊙O有几个？并请求出其中一个圆的半径．

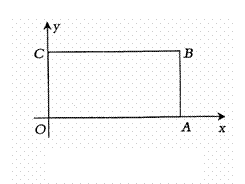
28、(本大题满分9分)把矩形纸片OABC放人直角坐标系中，使OA、OC分别落在x轴和y轴的正

半轴上．

(1)将纸片OAB C折叠，使点A与C重合，用直尺和圆规在原图上作出折叠后的

图形，并在图中标明折叠后点B的对应点B’(不写作法，保留作图痕迹)

(2)在矩形OABC中，连结AC，且AC=2，tan∠OAC=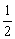，求A、C两点的坐标；并求(1)中折痕的长