
4.评分客观,适用于机器评分,减少评卷的劳动强度,确保了评分的客观性。
选择题最大的缺点,就是只能考查思维的结果,不能考查思维的过程,限制了创造力的考查,有一定的猜测性。
题型1 概念辨析型
有许多选择题,涉及了一些重要的数学概念、公式、定理、性质。或一些似是而非容易混淆的概念和性质,放在一起,迷惑同学们,这就需要同学们在审题时,特别注意辨析有关概念的本质特性,从而保证所选答案的正确性。一般说来,这类题目运算量小,侧重判断,下笔容易,但稍不留意则误入迷津。解这类题时常用的方法是:直接法、排除法、验证法等。
题型2 直接计算型
3.便于控制试题的难度。
2.可以根据考生易出现的问题,广泛地设置情景,能较好地进行有效测试。
选择题可以认为是一种最具典型性且最具测试功能的客观题,它有如下特点:
1.选择题解答方法简便,在单位时间内可以考查更广泛的学习内容,提高测验的效率。
 探索性问题分为规律探索型、存在探索型、条件探索型、结论探索型、综合探索型。此类问题的特点:问题的条件和结论不直接给出,需要通过观察、分析、概括、推理、判断等一系列探索活动,逐步确定要求的条件和结论。《课标》要求学生:能通过观察、实验、归纳、类比等获得数学猜想,并进一步寻求证据,给出证明或举出反例。探索性问题是符合课标要求的创新型问题。
探索性问题分为规律探索型、存在探索型、条件探索型、结论探索型、综合探索型。此类问题的特点:问题的条件和结论不直接给出,需要通过观察、分析、概括、推理、判断等一系列探索活动,逐步确定要求的条件和结论。《课标》要求学生:能通过观察、实验、归纳、类比等获得数学猜想,并进一步寻求证据,给出证明或举出反例。探索性问题是符合课标要求的创新型问题。
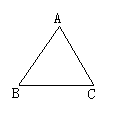
例如:△ABC是等边三角形,找一点P使△PAB、△PAC、△PBC都是等腰三角形,这样的点一共有多少个?
分析:此题属于存在探索型问题,需要对每一种情况进行猜想、论证,找到规律、分析要全面。它不仅考察学生的最基本的数学素养,也考察学生的归纳总结和创新实践能力。
这样就要求教师在教学中,从以往比较单一的教学方式,发展到开放性、创新性的教学方式,要求学生学会“问题--探究--发现--推广”的学习方式。这就要求教师教给学生:认真审题,通过对命题或式子的结构、特征、相应的图形等进行细致的研究,把握规律、合情推理、认真验证,从而得出问题的正确答案。
数学来源于生活,又应用于生活,能运用数学的思维方式观察、分析、解决日常生活和其他学科的相关问题,是每个公民应具备的基本素养。《标准》指出:“在经历知识的形成与应用过程中,更好地理解数学、发展应用意识和能力。关注学生能否结合具体情境发现并提出问题,能否尝试从不同角度分析和解决问题,能否解释结果的合理性,能否对解决问题的过程进行反思等。据调查,初中学生中半数不理解利润,看不懂股票走势图,弄不清统计图,不会填银行票据,更不会计算分期付款与一次性付款的利息问题,究其原因是在校内外学做家庭理财和参与社会服务的机会太少了,新课标重视数学学习与实践的结合,重视考察学生在面对真实情景下解决问题的能力,从而引导学生关注对应问题的领悟能力和解决能力。
例如:近两年某地外向型经济发展迅速,一些著名跨国公司纷纷落户该地新区,对各类人才需求不断增加,现一公司面向社会招聘人员,其信息如下:
[信息一]招聘对象:机械制造类和规划设计类人员共150名.
[信息二]工资待遇:机械类人员工资为600元/月,规划设计类人员为1000元/月.
设该公司招聘机械制造类和规划设计类人员分别为x人、y人.
(1)用含x的代数式表示y;
(2)若公司每月付给所招聘人员的工资为p元,要使本次招聘规划设计人员不少于机械制造人员的2倍,求p的取值范围.
分析:应用性问题是指有实际背景或问题有实际意义的数学问题,主要包括数与式应用、方程的应用、不等式的应用、函数的应用、统计知识的应用、几何知识的应用。此题目属于函数应用问题。要明确数量之间的关系,然后把数量关系转化成函数关系。
现在的数学应用问题可以说更加密切联系实际,在教学过程中要注意让学生多了解以下与数学有关的问题。例如股票、比赛等。同时,新教材带给了学生广阔的思维空间,转变了教师教学观念,通过数学建模将数学与应用问题紧紧地结合起来,对培养学生的问题意识、应用意识和探索意识,让学生主动关注身边的实际问题,应该说是开辟了一条行之有效的途径。
开放性问题分为条件开放型、结论开放型、情景开放型、方法策略开放型、综合开放型。“开放性”体现在:问题所提供的条件具有不确定性,解决问题的策略具有多样性,不同但合理的答案的多样性,问题结构的可变性等方面。《标准》强调关注学生的个性差异,有效地实施有差异性的教学,是每个学生都得到充分的发展,面对全体学生多元化的学习要求,开放性问题能较好地达到这一要求。在解决这类问题时,学生需要通过一系列分析,展开发散思维,运用所学知识经过推理,得出正确的结论。
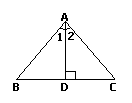 例如:如图,在△ABC中,AB=AC,AD⊥BC,D为垂足。由以上两个条件可得________。(写出一个结论)
例如:如图,在△ABC中,AB=AC,AD⊥BC,D为垂足。由以上两个条件可得________。(写出一个结论)
分析:这是一道探索、确定结论的开放型试题,解决这类问题的方法是根据条件,结合已学的知识、数学思想方法,通过分析、归纳逐步得出结论,或通过观察、实验、猜想、论证的方法求解。
在今后的教学中,通过开放性问题让学生经历适当的数学交流活动,感受到别人的思维方式和思维过程,以改变自己认识上的单一性。教师要加强“一题多解”“一题多变”“一题多用”“多题同法”“多题同果”等的训练,经过归纳、类比、模拟联想等推理地手段,得出正确结论。
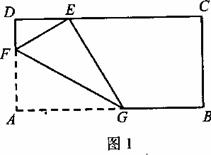
例4、(南京市2OO6年)已知矩形纸片ABCD,AB=2,AD=1,将纸片折叠,使顶点A与边CD上的点E重合.(1)如果折痕FG分别与AD、AB交与点F、G(如图1), ,求DE的长;
,求DE的长;
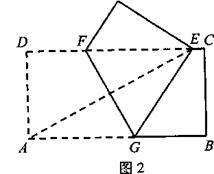
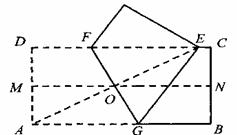
(2)如果折痕FG分别与CD、AB交与点F、G(如图2),△AED的外接圆与直线BC相切,
求折痕FG的长.
 解:⑴在矩形ABCD中,AB=2,AD=1AF=
解:⑴在矩形ABCD中,AB=2,AD=1AF=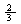 ,∠D=900.根据轴对称的性质得:EF=AF=
,∠D=900.根据轴对称的性质得:EF=AF= ,∵DF=AD-AF=
,∵DF=AD-AF=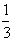 ,在RT△DEF中DE=
,在RT△DEF中DE=
 。
。
⑵设AE与FG的交点为O,根据轴对称的性质,得AO=EO,取AD的中点M,连接MO,则MO=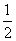 DE, MO∥DC,设DE=x,则MO=
DE, MO∥DC,设DE=x,则MO=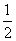 x,在矩形ABCD中,∠C=∠D=
x,在矩形ABCD中,∠C=∠D=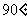 ,∴AE为
,∴AE为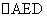 的外接圆的直径,O为圆心,延长MO交BC于点N,则ON∥CD,∴∠CNM=1800-∠C=
的外接圆的直径,O为圆心,延长MO交BC于点N,则ON∥CD,∴∠CNM=1800-∠C=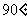 ,∴ON⊥BC,四边形MNCD是矩形,∴MN=CD=AB=2,∴ON=MN-MO=2-
,∴ON⊥BC,四边形MNCD是矩形,∴MN=CD=AB=2,∴ON=MN-MO=2-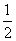 x,∵
x,∵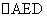 的外接圆与BC相切,∴ON是
的外接圆与BC相切,∴ON是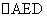 的外接圆的半径。∴OE=ON=2-
的外接圆的半径。∴OE=ON=2-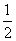 x,AE=2ON=4-x,在在RT△AED中,AD2+DE2=AE2,∴12+x2 =(4-x)2,解这个方程,得x=
x,AE=2ON=4-x,在在RT△AED中,AD2+DE2=AE2,∴12+x2 =(4-x)2,解这个方程,得x=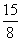 ,∴DE=
,∴DE=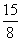 , OE=2-
, OE=2-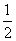 x=
x= ,
, 根据轴对称的性质,得AE⊥FG,∴∠FOE=∠D=
根据轴对称的性质,得AE⊥FG,∴∠FOE=∠D=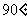 ,又∵∠FEO=∠AED,∴△FEO∽△AED, ∴
,又∵∠FEO=∠AED,∴△FEO∽△AED, ∴ ,∴
,∴ ,可得FO=
,可得FO= ,又∵AB∥CD,∴∠EFO=∠AGO,∠FEO=∠GAO,∴△FEO≌△GAO, ∴FO=GO, ∴FG=2FO=
,又∵AB∥CD,∴∠EFO=∠AGO,∠FEO=∠GAO,∴△FEO≌△GAO, ∴FO=GO, ∴FG=2FO=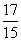 ,折痕的长是
,折痕的长是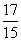 .
.
矩形纸沿某一直线对折这样的问题,需考虑折叠前后哪些量相同,哪些量变化了.此折叠问题与圆的切线、圆的外接圆、全等三角形、相似三角形、勾股定理、轴对称、矩形的判定等联系在一起,综合考查了学生的分析问题、解决问题的能力。
例3、(海淀区2006年)下列矩形中,按虚线剪开后,既能拼出平行四边形和梯形,又能拼出三角形的是图形. ________ (请填图形下面的代号)。
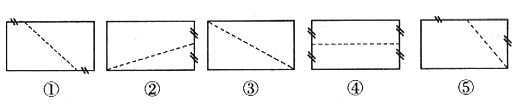
答案: ② 此题若学生把矩形纸按实际要求操作一下,答案很容易得到,但只凭想象答案很有可能出现多选情况。
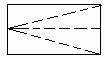
例2、(浙江省2006年) 现有一张长和宽之比为2:1的长方形纸片,将它折两次(第一次折后也可打开铺平再折第二次),使得折痕将纸片分为面积相等且不重叠的四个部分(称为一次操作),如图甲(虚线表示折痕).除图甲外,请你再给出三种不同的操作,分别将折痕画在图①至图③中(规定:一个操作得到的四个图形,和另一个操作得到的四个图形,如果能够“配对”得到四组全等的图形,那么就认为是相同的操作,如图乙和图甲示相同的操作).

 (甲)
(乙)
(甲)
(乙)
①
②
③


解析:

三、按要求拼接
此题考察了学生动手操作与创新的能力,学生必须转换角度,调整思路,灵活处理变化了的新问题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com