27、(1)设t秒时两点相遇，则有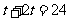，解得t=8，答：(略)……4分

(2)由(1)知，点N一直在AD上运动，所以当点M运动到BC边上的时候，点A、E、M、N才可能组成平行四边形。设：经过t秒，四点可组成平行四边形。分两种情形：……1分

a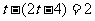．　 解得t=2　　　　　 ……4分

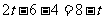b．　 解得t=6　　　　　 ……4分

答：第2秒或6秒钟时，点A、E、M、N组成平行四边形。……1分

26、(1)5　 ……………2分

(2)3小时两船相距240km…………………………………………2分

(3)y=120x-600(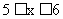)……………………………………2分

(4)设巡逻艇速度为xkm/h，货轮速度为ykm/h，

则两港距离为(3y+240)km…………………………………2分

　　 　　根据题意得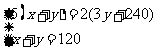： ……………………2分

求得：巡逻艇速度为100km/h，货轮速度为20km/h，两港距离300km

……2分

25．(1)28cm；(2)y=4x+4；(3)61 (各4分)

24．(1)利用sss(4分)；(2)AB∥CD或AD=BC等(2分)，理由4分。

22．画对角平分线、垂直平分线各4分。

21．(1)320，210，210(各1分)；(2)不合理，当出现异常数据时，平均数就不能较好地衡量集中趋势(1分)；(3)从众数、中位数说明(2分)

18.18；　 19.2；　　 20.71

13.50；　 14. 3；　 15. 24； 16．8或9cm　 　17.y=-x-3等；

27. (本小题满分14分)

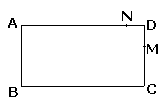
如图，矩形ABCD中，AB＝4cm，BC＝8cm，动点M从点D出发，按折线DCBAD方向以2cm/s的速度运动，动点N从点D出发，按折线DABCD方向以1cm/s的速度运动．

(1)若动点M、N同时出发，经过几秒钟两点相遇？

(2)若点E在线段BC上，BE＝2cm，动点M、N同时出发且相遇时均停止运动，那么点M运动到第几秒钟时，与点A、E、N恰好能组成平行四边形？

答案与提示

26、(12分)一艘巡逻艇与一艘货轮同时从甲港驶往乙港，巡逻艇不停地在甲、乙两港间巡逻，且巡逻艇和货轮的速度保持不变.设货轮行驶的时间为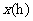，两船之间的距离为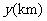，图中的折线

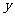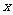表示与之间的函数关系．根据图象探究：

信息读取

(1)两船首次相遇需要　　　 小时；

(2)请解释图中点A的实际意义；

图象理解

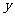(3)求线段所表示的与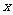之间的函数关系式；(不必写出自变量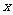的取值范围)

(4)求巡逻艇和货轮的速度以及甲、乙两港间的距离。