
(四)运用函数思想解决实际问题
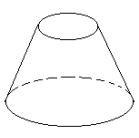 例5:一个圆台形物体的上底面积是下底面积的
例5:一个圆台形物体的上底面积是下底面积的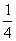 ,如果按下图放在桌上,对桌面的压强是200帕,翻过来放,对桌面的压强是多少?
,如果按下图放在桌上,对桌面的压强是200帕,翻过来放,对桌面的压强是多少?
(三)运用函数思想解不等式
例3:解不等式3x-6≥0
分析与解答:令y=3x-6,在平面直角坐标系中画出函数y=3x-6图象。
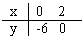
观察图象,3x-6≥0即函数值y≥0。函数值y≥0体现在图象上是在x轴上方部分(含直线与x轴交点),求3x-6≥0的解集就是求它所对应的自变量x的值,∴不等式3x-6≥0的解集是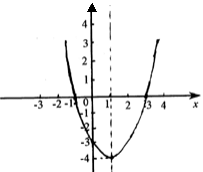 x≥2,这与直接解不等式结果相同。
x≥2,这与直接解不等式结果相同。
例4:解不等式x2-2x-3<0
分析与解答:令y=x2-2x-3,这里x2-2x-3<0实质上是函数y的值小于零。在平面直角坐标系中画出函数y=x2-2x-3的图象。
观察图象y<0体现在图象上是x轴下方部分,∴不等式x2-2x-3<0的解集是-1<x<3.另外通过观察图象还可以得出不等式x2-2x-3>0的解集是x<-1或x>3。
(二)运用函数思想解方程组
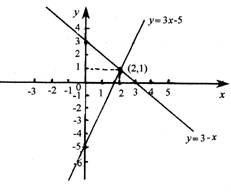 例2:利用函数图象解二元一次方程组。
例2:利用函数图象解二元一次方程组。
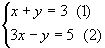 分析与解答:由(1)得y=3-x,由(2)得y=3x-5,这实质是两个y与x之间的一次函数,在平面直角坐标系中先画出这两条直线。
分析与解答:由(1)得y=3-x,由(2)得y=3x-5,这实质是两个y与x之间的一次函数,在平面直角坐标系中先画出这两条直线。
(1)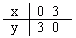 (2)
(2)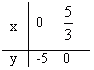
两条直线有一个交点,交点的坐标就表示两个方程的公共解,交点的坐标是(2,1),所以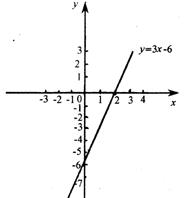 原方程组的解是
原方程组的解是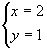 ,这与用代入法或加减法解得的结果相同。
,这与用代入法或加减法解得的结果相同。
(一)运用函数思想求最值
例1:如图:一个矩形ABCD,它的周长为20cm,当边长为多少时,矩形的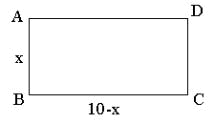 面积最大,最大面积是多少?
面积最大,最大面积是多少?
分析与解答:运用函数思想,应首先构造一个函数。令AB=xcm,则BC=(10-x)cm.因此矩形面积y=x(10-x). 面积y是边长x的二次函数,y=-x2+10x,经过配方:y=-(x-5)2+25. ∴当x=5cm时,y的最大值是25cm2,实质上这时四边形ABCD是一个正方形,即当边长AB=5cm时,矩形面积最大,最大面积是25cm2.
例1.已知P(m, n)是一次函数y=-x+1图象上的一点,二次函数y=x2+mx+n的图象与x轴两个交点的横坐标的平方和为1,问点N(m+1, n-1)是否在函数y=-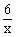 图象上。
图象上。
分析:P(m, n)是图象上一点,说明P(m, n)适合关系式y=-x+1,代入则可得到关于m,n的一个关系,二次函数y=x2+mx+n与x轴两个交点的横坐标是方程x2+mx+n=0的两个根,则x1+x2=-m, x1x2=n, 由平方和为1即x12+x22=(x1+x2)2-2x1x2=1,又可得到关于m, n的一个关系,两个关系联立成方程组,可解出m, n,这种利用构造方程求函数系数的思想最为常见。
解:∵P(m,n)在一次函数y=-x+1的图象上,
∴ n=-m+1, ∴ m+n=1.
设二次函数y=x2+mx+n的图象与x轴的两个交点的横坐标为x1,x2,
∴x12+x22=1,
又∵x1+x2=-m, x1x2=n,
∴ (x1+x2)2-2x1x2=1, 即m2-2n=1
由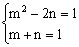 解这个方程组得:
解这个方程组得: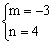 或
或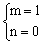 。
。
把m=-3, n=4代入x2+mx+n=0,
x2-3x+4=0, Δ<0.
∴ m=-3, n=4(舍去).
把m=1, n=0代入x2+mx+n=0,
x2+x=0, Δ>0
∴点N(2,-1),
把点N代入y=-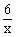 ,当x=2时,y=-3≠-1.
,当x=2时,y=-3≠-1.
∴点N(2,-1)不在图象y=-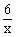 上。
上。
说明:这是一道综合题,包括二次函数与一次函数和反比例函数,而且需要用到代数式的恒等变形,与一元二次方程的根与系数关系结合,求出m、n值后,需检验判别式,看是否与x轴有两个交点。当m=-3, n=4时,Δ<0,所以二次函数与x轴无交点,与已知不符,应在解题过程中舍去。是否在y=-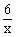 图象上,还需把点(2,-1)代入y=-
图象上,还需把点(2,-1)代入y=-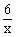 ,满足此函数解析式,点在图象上,否则点不在图象上。
,满足此函数解析式,点在图象上,否则点不在图象上。
例2.直线 y=-x与双曲线y=-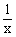 的两个交点都在抛物线y=ax2+bx+c上,若抛物线顶点到y轴的距离为2,求此抛物线的解析式。
的两个交点都在抛物线y=ax2+bx+c上,若抛物线顶点到y轴的距离为2,求此抛物线的解析式。
分析:两函数图象交点的求法就是将两函数的解析式联立成方程组,方程组的解既为交点坐标。
解:∵直线y=-x与双曲线y=-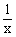 的交点都在抛物线y=ax2+bx+c上,
的交点都在抛物线y=ax2+bx+c上,
由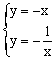 解这个方程组,得x=±1.
解这个方程组,得x=±1.
∴当x=1时,y=-1.
当x=-1时,y=1.
经检验: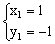 ,
,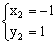 都是原方程的解。
都是原方程的解。
设两交点为A、B,∴A(1,-1),B(-1,1)。
又∵抛物线顶点到y轴的距离为2,∴ 抛物线的对称轴为直线x=2或x=-2,
当对称轴为直线x=2时,
设所求的抛物线解析式为y=a(x-2)2+k,又∵过A(1,-1),B(-1,1),
∴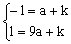 解方程组得
解方程组得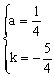
∴ 抛物线的解析式为y=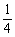 (x-2)2-
(x-2)2-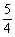
即 y=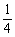 x2-x-
x2-x-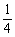 .
.
当对称轴为直线x=-2时,设所求抛物线解析式为y=a(x+2)2+k,
则有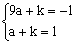 解方程组得
解方程组得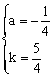 ,
,
∴ 抛物线解析式为y=-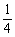 (x+2)2+
(x+2)2+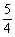
y=-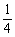 x2-x+
x2-x+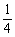 .
.
∴所求抛物线解析式为:y=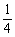 x2-x-
x2-x-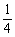 或y=-
或y=-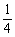 x2-x+
x2-x+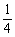 。
。
说明:在求直线和双曲线的交点时,需列出方程组,通过解方程组求出x, y值,双曲线的解析式为分式方程,所以所求x, y值需检验。抛物线顶点到y轴距离为2,所以对称轴可在y轴左侧或右侧,所以要分类讨论,求出抛物线的两个解析式。
例3、已知∠MAN=30°,在AM上有一动点B,作BC⊥AN于C,设BC的长度为x,△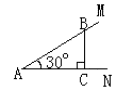 ABC的面积为y,试求y与x之间的函数关系式。
ABC的面积为y,试求y与x之间的函数关系式。
分析:求两个变量y与x之间的函数关系式,就是想办法用x表示y,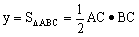 ,BC=x,则想办法先用含x的代数式表示AC。
,BC=x,则想办法先用含x的代数式表示AC。
解:如图 在Rt△ABC中, ∵∠A=30°,∠BCA=90° BC=x,
∴AC=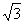 BC=
BC=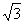 x ∴
x ∴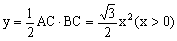
说明:在含有30°、45°、60°的直角三角形中,应注意利用边之间的特殊倍数关系(如AC=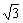 BC)。
BC)。
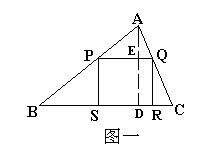 例4、如图,锐角三角形ABC的边长BC=6,面积为12,P在AB上,Q在AC上,且PQ∥BC,正方形PQRS的边长为x,正方形PQRS与△ABC的公共部分的面积为y。
(1)当SR恰落在BC上时,求x,
(2)当SR在△ABC外部时,求y与x间的函数关系式;
(3)求y的最大值。
例4、如图,锐角三角形ABC的边长BC=6,面积为12,P在AB上,Q在AC上,且PQ∥BC,正方形PQRS的边长为x,正方形PQRS与△ABC的公共部分的面积为y。
(1)当SR恰落在BC上时,求x,
(2)当SR在△ABC外部时,求y与x间的函数关系式;
(3)求y的最大值。
略解:(1)由已知,△ABC的高AD=4。
 ∵△APQ∽△ABC,(如图一)
∵△APQ∽△ABC,(如图一)
设AD与PQ交于点E ∴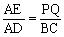 ∴
∴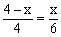 ∴
∴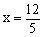
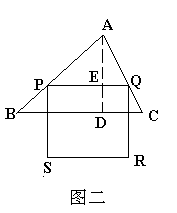
(2)当SR在△ABC的外部时, 同样有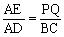 ,
则
,
则 ,即AE=
,即AE=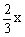
∴y=ED·PQ=x(4-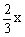 )=-
)=-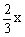 2+4x(
2+4x(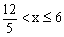 )
)
(3)∵a=-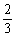 <0,y=-
<0,y=-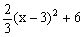 其中
其中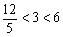 ,
,
∴当x=3时,y取得最大值6.
说明:此例将线段PQ的长设为x,正方形PQRS与△ABC的公共部分的面积设为y,寻找它们之间的函数关系.注意自变量的取值范围;在y取最大值时,要注意顶点(3,6)的横坐标是否在取值范围内.
例5.( 潍坊市中考题)某公园草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m加设不锈钢管(如图一)作成的立柱。为了计算所需不锈钢管立柱的总长度,设计人员利用图二所示的坐标系进行计算。 (1)求该抛物线的解析式; (2)计算所需不锈钢管立柱的总长度。
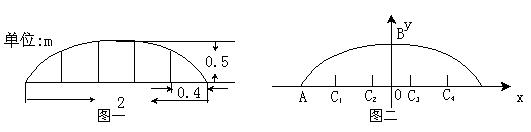
分析:图中给出了一些数量,并已经过护栏中心建立了平面直角坐标系, 所以求二次函数的解析式关键是找到一些条件建立方程组。因为对称轴是 y轴,所以b=0,可以设二次函数为y=ax2+c.
解:(1)在如图所示坐标中,设函数解析式为y=ax2+c,B点坐标为(0,0.5),C点坐标为(1,0)。
分别代入y=ax2+c得: 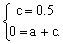 ,解得
,解得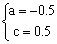 抛物线的解析式为:y=-0.5x2+0.5
抛物线的解析式为:y=-0.5x2+0.5
(2)分别过AC的五等分点,C1,C2,C3,C4,作x轴的垂线,交抛物线于B1,B2,B3,B4,则C1B1,C2B2,C3B3,C4B4的长就是一段护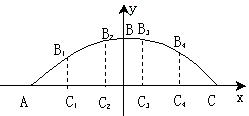 栏内的四条立柱的长,点C3,C4的坐标为(0.2,0)、(0.6,0),则B3,B4点的横坐标分别为x3=0.2,x4=0.6.
将x3=0.2和x4=0.6分别代入 y=-0.5x2+0.5得y3=0.48,y4=0.32
栏内的四条立柱的长,点C3,C4的坐标为(0.2,0)、(0.6,0),则B3,B4点的横坐标分别为x3=0.2,x4=0.6.
将x3=0.2和x4=0.6分别代入 y=-0.5x2+0.5得y3=0.48,y4=0.32
由对称性得知,B1,B2点的纵坐标:y1=0.32,y2=0.48
四条立柱的长为:C1B1=C4B4=0.32(m) C2B2=C3B3=0.48(m) 所需不锈钢立柱的总长为 (0.32+0.48)×2×50=80(m)。
答:所需不锈钢立柱的总长为80m。
1.(徐州市)函数y=ax2+a与y=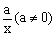 在同一坐标系中的图像可能是:( )
在同一坐标系中的图像可能是:( )
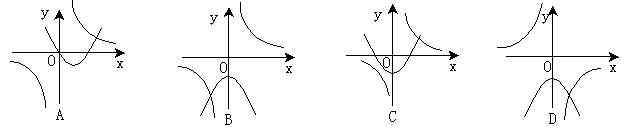
分析:当a>0时,函数y=ax2+a与y=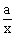 的图象应满足性质
图象y=ax2+a ①开口向上;②与y轴交点(0, a)在y轴正半轴;③对称轴为y轴
图象y=
的图象应满足性质
图象y=ax2+a ①开口向上;②与y轴交点(0, a)在y轴正半轴;③对称轴为y轴
图象y=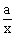 应满足双曲线在一、三象限 从A、C中,A明显不合题意,对称轴不是y轴
C中抛物线与y轴交点(0, a)不在y轴的正半轴 当a<0时,从B、D中选择。
a<0图象y=ax2+a特点是①开口向下;②对称轴y轴;③与y轴交点(0, a)在y轴的负半轴。
图象y=
应满足双曲线在一、三象限 从A、C中,A明显不合题意,对称轴不是y轴
C中抛物线与y轴交点(0, a)不在y轴的正半轴 当a<0时,从B、D中选择。
a<0图象y=ax2+a特点是①开口向下;②对称轴y轴;③与y轴交点(0, a)在y轴的负半轴。
图象y=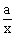 特点,双曲线在二、四象限, 故选D。也可以一个个图象依次分析。
特点,双曲线在二、四象限, 故选D。也可以一个个图象依次分析。
2.(扬州市)已知四点A(1,2),B(3,0),C(-2,20),D(-1,12)。试问,是否存在一个二次函数,使它的图像同时经过这四点。如果存在,请求出它的解析式;如果不存在,请说明理由。
分析:可以通过三点先确定一个抛物线,再考察第四个点是否满足抛物线的解析式。若满足,则可确定同时过四点的抛物线;若不满足,则不存在同时过四点的抛物线。
解:设二次函数y=ax2+bx+c的图像经过A、B、D三点
则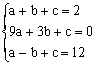 ,解得
,解得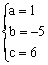 即二次函数y=x2-5x+6的图像通过A、B、D三点,经计算C(-2,20)的坐标也满足上式,因此点D也在此函数图像上,故存在一个二次函数y=x2-5x+6,它的图象同时经过A、B、C、D四点。
即二次函数y=x2-5x+6的图像通过A、B、D三点,经计算C(-2,20)的坐标也满足上式,因此点D也在此函数图像上,故存在一个二次函数y=x2-5x+6,它的图象同时经过A、B、C、D四点。
3.( 苏州市)已知:一次函数y=2x+k-3和反比例函数y=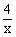 的图像都经过点A(n,2)。
(1)求n的值和这个一次函数的解析式;
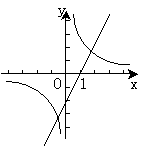
(2)在下边的坐标系中画出这两个函数的大致图像(不必列表);
(3)根据图像判断:使这两个函数的值的都为非负数的自变量x的取值范围是 。
的图像都经过点A(n,2)。
(1)求n的值和这个一次函数的解析式;
(2)在下边的坐标系中画出这两个函数的大致图像(不必列表);
(3)根据图像判断:使这两个函数的值的都为非负数的自变量x的取值范围是 。
 (1)解:∵
(1)解:∵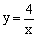 的图像过点A(n,2), ∴2=
的图像过点A(n,2), ∴2=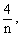 ∴n=2
∵一次函数的图像过点A(2,2), ∴2=4+k-3, ∴k=1 ∴它的解析式为y=2x-2
∴n=2
∵一次函数的图像过点A(2,2), ∴2=4+k-3, ∴k=1 ∴它的解析式为y=2x-2
(2)(画出两个函数的大致图像各得1分) (3)x≥1.
4.(天门市)如图,已知抛物线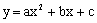 与x轴负半轴交于A、B两点,与y轴交于点C,且
与x轴负半轴交于A、B两点,与y轴交于点C,且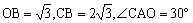 ,求抛物线的解析式和它的顶点坐标。
,求抛物线的解析式和它的顶点坐标。
 分析:确定抛物线的解析式,通常需要三个条件。图中已知一些线段OB、CB的长,并知道∠CAO=30°,由此可以求出A、B、C三点坐标。
分析:确定抛物线的解析式,通常需要三个条件。图中已知一些线段OB、CB的长,并知道∠CAO=30°,由此可以求出A、B、C三点坐标。
解:在RtΔBOC中,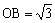 ,
,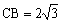 ∴
∴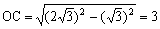 在RtΔAOC中,∠CAO=30
∴
在RtΔAOC中,∠CAO=30
∴ ∴A
∴A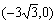 ,B
,B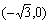 ,C(0,3)
,C(0,3)
(注意:将线段的长度转化为点的坐标时,一定要根据条件添加符号;反过来将坐标转化为线段的长度时,要加绝对值。) ∵A、B、C三点在抛物线上
∴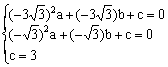 ,解得
,解得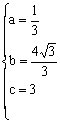 ∴抛物线的解析式为:
∴抛物线的解析式为: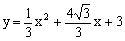 ∵y=
∵y=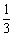 x2+
x2+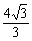 x+3=
x+3=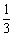 (x2+4
(x2+4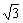 x+9)=
x+9)=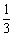 [(x+2
[(x+2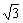 )2-(2
)2-(2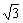 )2+9]=
)2+9]=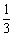 (x+2
(x+2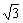 )2-1
∴抛物线的顶点坐标为
)2-1
∴抛物线的顶点坐标为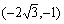
5.(石家庄市)一河流每小时流入水库2千m3水,到春天需由水库开闸放水灌溉麦田,若开闸时水库恰好蓄水2亿m3,并且开闸时每小时放水4千m3。 (1)求水库的蓄水量y与灌溉时间t之间的函数关系式; (2)已知每公顷小麦灌溉一次大约需用水1千m3,若水库的畜水量在灌溉期间其存水量必须不能少于100万m3水,这样,求水库的水最多能连续灌溉多少公顷麦田。
分析:此题是函数方面的应用题,所谓函数,就是两个变量之间的关系,与列方程一样,将两个变量之间的关系列出,另外一定要注意题目中的数量换算。 在解题时可将水的单位统一为千m3
解:(1)y=200000+(2-4)t =200000-2t(t>0),(y的单位是千m3)
(2)200000-2t≥1000 ∴t≤99500(小时)
灌溉1公顷麦田需用时间t'=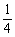 小时 ∴995000÷
小时 ∴995000÷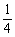 =3980000(公顷)
=3980000(公顷)
答:水库的水最多能连续灌溉3980000公顷麦田。
5.(徐州市)设x1、x2是方程2x2-4mx+(2m2-4m-3)=0的两个实数根。
(1)若y=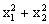 ,求y与m之间的函数关系式及自变量m的取值范围;
(2)画出第(1)题中函数y的图像,观察图像,说明函数y有没有最小值或最大值,如果有,求出最大值或最小值;如果没有,说明理由。
,求y与m之间的函数关系式及自变量m的取值范围;
(2)画出第(1)题中函数y的图像,观察图像,说明函数y有没有最小值或最大值,如果有,求出最大值或最小值;如果没有,说明理由。
解:(1)x1+x2=2m,x1x2=m2-2m-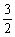
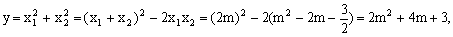 ∵△=(-4m)2-4×2×(2m2-4m-3)
=16m2-16m2+32m+24 =32m+24
由△≥0,得m≥-
∵△=(-4m)2-4×2×(2m2-4m-3)
=16m2-16m2+32m+24 =32m+24
由△≥0,得m≥-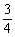 ,∴y=2m2+4m+3(m≥-
,∴y=2m2+4m+3(m≥-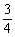 )
)
(2)画图略。观察图像可知,当m≥-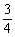 时,y随m的增大而增大,
∴m=-
时,y随m的增大而增大,
∴m=-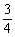 时,y有最小值为
时,y有最小值为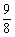 ,y没有最大值。(正确画出图像,得2分。“有最小值”、“没有最大值”各1分)。
,y没有最大值。(正确画出图像,得2分。“有最小值”、“没有最大值”各1分)。
函数思想的应用
函数的实质是研究两个变量之间的对应关系,灵活运用好函数思想能解决许多数学问题。
4.二次函数y=ax2与y=a(x-h)2+k的关系:图象开口方向相同,大小、形状相同,只是位置不同。y=a(x-h)2+k图象可通过y=ax2平行移动得到。当h>0时,向右平行移动|h|个单位;h<0向左平行移动|h|个单位;k>0向上移动|k|个单位;k<0向下移动|k|个单位;也可以看顶点的坐标的移动, 顶点从(0,0)移到(h,k),由此容易确定平移的方向和单位。
3.对于二次函数解析式,除了掌握一般式即:y=ax2+bx+c((a≠0)之外,还应掌握“顶点式”y=a(x-h)2+ k及“两根式”y=a(x-x1)(x-x2),(其中x1,x2即为图象与x轴两个交点的横坐标)。当已知图象过任意三点时,可设“一般式”求解;当已知顶点坐标,又过另一点,可设“顶点式”求解;已知抛物线与x轴交点坐标时,可设“两根式”求解。总之,在确定二次函数解析式时,要认真审题,分析条件,恰当选择方法,以便运算简便。
四种常见函数的图象和性质总结
|
|
图象 |
特殊点 |
性质 |
|
一 次 函 数 |
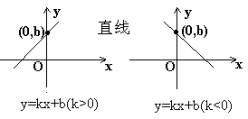 |
与x轴交点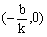 与y轴交点(0,b) |
(1)当k>0时,y随x的增大而增大; (2)当k<0时,y随x的增大而减小. |
|
正 比 例 函 数 |
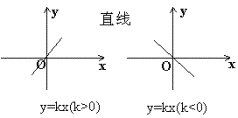 |
与x、y轴交点是原点(0,0)。 |
(1)当k>0时,y随x的增大而增大,且直线经过第一、三象限; (2)当k<0时,y随x的增大而减小,且直线经过第二、四象限 |
|
反 比 例 函 数 |
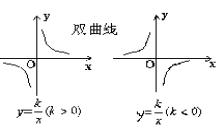 |
与坐标轴没有交点,但与坐标轴无限靠近。 |
(1)当k>0时,双曲线经过第一、三象限,在每个象限内,y随x的增大而减小; (2) 当k<0时,双曲线经过第二、四象限,在每个象限内,y随x的增大而增大。 |
|
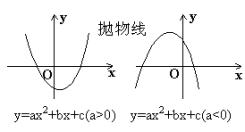
二 次 函 数 |
 |
与x轴交点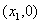 或 或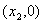 ,其中 ,其中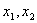 是方程 是方程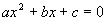 的解,与y轴交点 的解,与y轴交点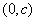 ,顶点坐标是 (- ,顶点坐标是 (-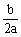 , , )。 )。 |
(1)当a>0时,抛物线开口向上,并向上无限延伸;对称轴是直线x=-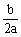 , y最小值= , y最小值= 。 。 (2)当 a<0时,抛物线开口向下,并向下无限延伸;对称轴是直线x=- 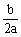 , y最大值= , y最大值= |
方法有两种,一种是直接利用定义,结合几何直观图形,先求出有关垂线段的长,再根据该点的位置,明确其纵、横坐标的符号,并注意线段与坐标的转化,线段转换为坐标看象限加符号,坐标转换为线段加绝对值;另一种是根据该点纵、横坐标满足的条件确定,例如直线y=2x和y=-x-3的交点坐标,只需解方程组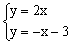 就可以了。
就可以了。
2.对解析式中常数的认识:
一次函数y=kx+b (k≠0)、二次函数y=ax2+bx+c(a≠0)及其它形式、反比例函数y= (k≠0),不同常数对图像位置的影响各不相同,它们所起的作用,一般是按其正、零、负三种情况来考虑的,一定要建立起图像位置和常数的对应关系。
(k≠0),不同常数对图像位置的影响各不相同,它们所起的作用,一般是按其正、零、负三种情况来考虑的,一定要建立起图像位置和常数的对应关系。
28.(本题满分10分)
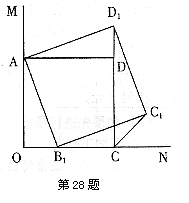
如图:∠MON =90°,在∠MON的内部有一个正方形AOCD,点A、C分别在射线OM、ON上,点B1是ON上的任意一点,在∠MON的内部作正方形AB1C1D1。
(1)连续D1D,求证:∠ADD1 = 90°;
(2)连结CC1,猜一猜,∠C1CN的度数是多少?并证明你的结论;
(3)在ON上再任取一点B2,以AB2为边,在∠MON的内部作正方形AB2C2D2,观察图形,并结合(1)、(2)的结论,请你再做出一个合理的判断。
27.(本题满分10分)
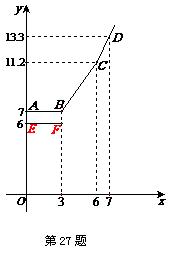
为缓解油价上涨给出租车行业带来的成本压力,某市自2008年1月10日起,调整出租车运价,调整方案见下列表格及图象(其中a、b、c为常数):
|
行驶路程 |
收费标准 |
|
|
调价前 |
调价后 |
|
|
不超出3 km的部分 |
起步价6元 |
起步价a元 |
|
超出3 km不超出6 km的部分 |
每公里2.1元 |
每公里b元 |
|
超出6 km的部分 |
每公里c元 |
设行驶路程为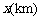 时,调价前的运价为
时,调价前的运价为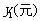 ,调价后的运价为
,调价后的运价为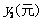 .如图,折线
.如图,折线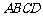 表示y2与x之间的函数关系;线段EF表示0≤x≤3时,y1与x之间的函数关系.根据图表信息,完成下列各题:
表示y2与x之间的函数关系;线段EF表示0≤x≤3时,y1与x之间的函数关系.根据图表信息,完成下列各题:
(1)填空: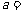 ,
,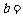 ,
,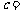 ;
;
(2)写出当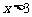 时,
时,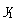 与x之间的函数关系式,并在上图中画出该函数图象;
与x之间的函数关系式,并在上图中画出该函数图象;
(3)函数y1 与y2的图象是否存在交点?若存在,求出交点坐标,并说明该点的实际意义.若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com