5．一元二次方程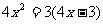的根的情况是　　　　　　　　　 ．

4．若是方程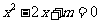的一个根，则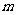的值为　　　 ，另一个根为　　　　　　　 。

3．若方程是一元二次方程，当m满足条件　　　　 。

2．平面直角坐标系内一点P(－2，3)关于原点对称点的坐标是　　　　　 ．

1．当　　时，有意义．

28．解：(1)图形平移的距离就是线段BC的长(2分)

又∵在Rt△ABC中，斜边长为10cm，∠BAC=30，∴BC=5cm，

平移的距离为5cm．(2分)

(2)∵∠FA＝30°，∴∠，∠D=30°．∴∠．

在RtEFD中，ED=10 cm，∵FD=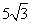， ∵cm．

28．(8分)如图1，小明将一张矩形纸片沿对角线剪开，得到两张三角形纸片(如图2)，量得他们的斜边长为10cm，较小锐角为30°，再将这两张三角纸片摆成如图3的形状，但点B、C、F、D在同一条直线上，且点C与点F重合(在图3至图6中统一用F表示)

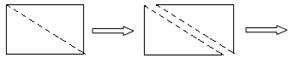
　　 　　　(图1)　　　　　　　 (图2)　　　　　　 (图3)

小明在对这两张三角形纸片进行如下操作时遇到了三个问题，请你帮助解决。

(1)将图3中的△ABF沿BD向右平移到图4的位置，使点B与点F 重合，请你求出平移的距离；

(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置，A₁F交DE于点G，请你求出线段FG的长度；

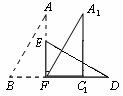
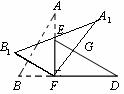
(图4)　　　　　　 (图5)　　　　　　　 (图6)

27．(6分)(1)如图()，它是一个多么漂亮的图案啊!请你在这个图案中确定一个基本图形，然后说出这个基本图形经过怎样的变换便可得到图()；

(2)如图(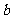)，将它分成，△OAB、△OBC、△OCD等三个等边三角形(包含三角形内部所有图形)．

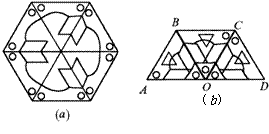①探究：△OAB怎样变换可以得到△OBC?△OBC怎样变换可以得到△OCD?△OAB怎样变换可以得到△OCD?

②思考：对称与旋转有何关系?

26．(6分)如图15-28所示，是正方形内一点，△ABP经旋转能与△CBP′重合，求：

　 (1)旋转中心是哪个点？

(2)旋转了多少度？

(3)若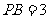，求的面积。

25．(6分)如图，正方形ABCD中，E为BC边上的一点，将△ABE旋转后得到△CBF．

　 (1)指出旋转中心及旋转的角度；

　　(2)判断AE与CF的位置关系；

(3)如果正方形的面积是18cm²，△BCF的面积是5cm²，问四边形AECD的面积是多少？