35、　 二元一次方程组的解法：

方法一：代入法

方法二：加减法

34、　 二元一次方程组的解：使二元一次方程组的两个方程左右两边的值都相等的两个未知数的值，叫做二元一次方程组的解。

33、　 根系关系：若

　　　　　　 则

32、　 根的判别式：

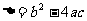
31、　 等式的两条基本性质：

①　　 等式两边同时加上或减去一个整式，等号仍然成立。

②　　 等式两边同时乘以或除以一个不等于零的整式，等号仍然成立。

30、　 无理方程的解法：

①　　 将它两边乘方化成有理方程去解，解出后要检验它的根。

②　　 换元，设出辅助未知数。

29、　 分式方程的解法：

①　　 在方程的两边都乘以最简公分母，约去分母，化成整式方程；

②　　 解这个整式方程；

③　　 把整式方程的根代入最简公分母进行检验。最简公分母=0时为增根，舍去；最简公分母≠0时，为原分式方程的解。

28、　 一元二次方程的解法(举例)：

①　　 因式分解法把方程的一边化为零，另一边因式分解，令每个因式为零，解每个方程．所有的解，就是原方程的解。ax²+bx+c=0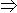a(x－x₁)(x－x₂)=0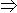． x－x₁=0或x－x₂＝0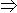． x=x₁或x=x₂。

②　　 把开方数化成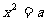的形式，两边同时开放得。

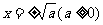③　　 配方法用二次项的系数除方程的两边各项；把二次项和一次项移到方程的左边，常数项移到方程的右边；方程两边各加上一次项系数的一半的平方，方程左边变成一个二项式的完全平方，右边化成一个常数项；方程两边同时开方，得到两个一次方程；分别解这两个一次方程，求出两个根。

④　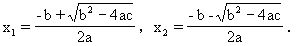　 公式法ax²+bx+c＝0(a≠0)

27、　 一元一次方程的解法：

①去分母：方程两边同乘以各分母的最小公倍数。

②去括号。

③移项：从方程一边移到另一边项要改变性质符号。

④合并同类项，化成最简方程ax=b(a≠0)的形式。

⑤方程两边都除以未知数的系数．得出方程的解。

26、　 方程的增根：在方程变形中，有时产生不适合原方程的根，这种根叫做原方程的增根。