
2、分解因式: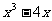 = .
= .
1、2006的相反数是 .
4、大大小小解没了
如果不等式组中两个不等式的解集分别是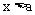 和
和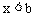 ,并且
,并且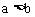 ,那么这个不等式组无解。
,那么这个不等式组无解。
例4 解不等式组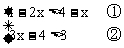
解:解不等式①,得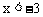 ;解不等式②,得
;解不等式②,得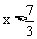 。两个不等式解集的不等号方向相反,并且是x大于两个数中的较大的数,同时小于较小的数。根据“大大小小解没了”,所以这个不等式组无解。
。两个不等式解集的不等号方向相反,并且是x大于两个数中的较大的数,同时小于较小的数。根据“大大小小解没了”,所以这个不等式组无解。
把不等式①和②的解集在同一数轴上表示出来,对以上结果进行验证。如图4,显然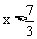 和
和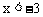 没有公共部分,所以原不等式组无解。
没有公共部分,所以原不等式组无解。
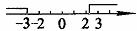
图4
3、大小小大中间找
如果不等式组中两个不等式的解集分别是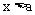 和
和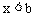 ,并且a<b,则此不等式组的解集是
,并且a<b,则此不等式组的解集是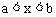 。
。
例3 解不等式组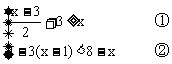
解:解不等式①,得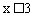 ;解不等式②,得
;解不等式②,得 。
。
两个不等式的解集一个是大于号,一个是小于等于号,并且是x大于两个数中较小的数-2,小于等于较大的数3。根据“大小小大中间找”,这个不等式组的解集是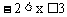 。
。
把不等式①和②的解集在同一数轴上表示出来,对以上结果进行验证。如图3,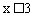 和
和 的公共部分是
的公共部分是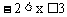 。
。

图3
2、同小取小
若一个不等式组中两个不等式的解集分别是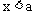 和
和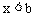 ,并且
,并且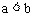 ,那么
,那么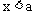 就是此不等式组的解集。
就是此不等式组的解集。
例2 解不等式组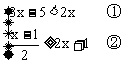
解:解不等式①,得x<5;解不等式②,得 。
。
显然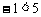 ,又两个不等式的解集一个是小于号,另一个是小于等于号,根据“同小取小”的口诀,这个不等式组的解集是
,又两个不等式的解集一个是小于号,另一个是小于等于号,根据“同小取小”的口诀,这个不等式组的解集是 。
。
把不等式①和②的解集在同一数轴上表示出来,对以上结果进行验证。如图2, 和
和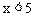 的公共部分是
的公共部分是 ,所以原不等式组的解集为
,所以原不等式组的解集为 。
。
图2
1、同大取大
如果一个不等式组中两个不等式的解集分别是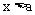 和
和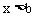 ,并且
,并且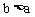 ,那么这个不等式组的解集是
,那么这个不等式组的解集是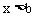 。
。
例1 解不等式组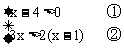
解:解不等式①,得x>4;解不等式②,得 。
。
显然 ,又两个不等式的解集中都是大于号,根据“同大取大”的口诀,所以这个不等式组的解集是x>4。
,又两个不等式的解集中都是大于号,根据“同大取大”的口诀,所以这个不等式组的解集是x>4。
把不等式①和②的解集在同一数轴上表示出来,对以上结果进行验证。如图1,显然 和x>4的公共部分是
和x>4的公共部分是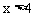 ,所以原不等式组的解集为x>4。
,所以原不等式组的解集为x>4。
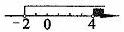
图1
2、如果把某个自然数任意计算它的N次方后,得到的各种结果的末A位数与原自然数的末A位数相同,我们就称这个自然数为“永恒数”, 例如:一位自然数的永恒数有1,5,6三个; 两位的永恒数一个是25, 另一个是101-25=76; 三位的永恒数是25的平方625,还有一个是1001-625=376; 四位的永恒数是625的平方90625的末四位:0625,与10001-0625=9376,由于的首位是0,实际只有一个9376, 五位的永恒数是90625与100001-90625=09376,实际只有一个90625,9376的平方87909376的末五位数是09376,用100001-09376=90625, 六位的永恒数是--------------- 从上面能否发现一些永恒数的规律: 从两位数开始永恒数一般只有两个且成对出现(当首位出现0时例外),每一对永恒数的结果总等于10??01(比这对永恒数的位数多一位)。
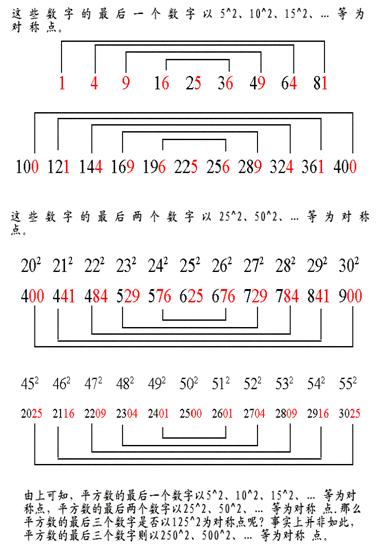
与完全平方数的末几位数有关的数字问题:
1、完全平方数的末两位数字只能是00;01,21,41,61,81;04,24,44,64,84; 25;16,36,56,76,96;09,29,49,69,89共22种可能
46.设1/a+1/b=1/c,其中a、b、c是正整数,且三个数的最大公因数是1,求证: a+b是一个完全平方数
45.自然数N是完全平方数。N不是10的倍数,但把N最后两位数字擦去,剩下的刚巧还是完全平方数(例如N可以是121,把21擦去,剩下的1还是完全平方数)。问N最大是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com