
有些例题,题型新颖、综合,难度较大,学生往往对此一筹莫展。因此,例题教学时,应根据题目特点,找准突破口,巧妙降低难度。将大题化小,深题化浅,让学生豁然开朗。
例如:二次函数y=(a+b)x2+2cx-a+b中,a、b、c是△ABC的三边,且当x=- 时,这个函数的最小值为-
时,这个函数的最小值为- ,试判断此三角形的形状。
,试判断此三角形的形状。
面对此题很容易从二次函数的最值公式入手去考虑系得出待定子数a、b、c三边关系,但该题如此解,题量很大,计算繁杂,易错难解。若换一角度,从解析式入手,采用逆向思维,问题便可迎刃而解了。
解:设二次函数解析式为y=(a+b)(x+ )2-
)2- =(a+b)x2+(a+b)x+
=(a+b)x2+(a+b)x+ 与原解析式y=(a+b)x2+2cx-a+b对比,∴a+b=2c,
与原解析式y=(a+b)x2+2cx-a+b对比,∴a+b=2c, =-a+b ∴a=b=c,即△ABC是正三角形。
=-a+b ∴a=b=c,即△ABC是正三角形。
例题、习题的讲解方法很多,本文只列举了常见的几种。总之,只要我们充分利用复习课的可塑空间,根据复习内容的特点,灵活选择与创新设计例题、习题,使例题、习题在复习课中起到以例代类、举一反三的作用,数学复习课教学必将取得良好成效。
有些例题,题设条件中虽然不同,但思考的方法、解决的途径却是相通的。能将一题进行适当变换,让学生在变中寻求不变,这对学生思维的开拓发散必有益处,对处在紧张复习阶段的学生从“题海”中解脱无疑也是一个很好的策略。如果我们教师在平常的复习、备课中注意这方面的研究,对学生在短时间内提高成绩、培养能力定能起积极作用。
例如:下面一题的条件经两次变换:如图,两等圆⊙O1、⊙O2相交于A、B两点,且两圆互相过圆心,过B作任一直线,分别交⊙O1、⊙O2于C、D两点,连接AC、AD
⑴ 试猜想△ABC的形状,并给出证明;
⑵ 若已知条件中的两圆不一定互相过圆心,试猜想三角形的形状是怎样的?证明你的结论。
 ⑶ 若⊙O1、⊙O2是两个不相等的圆,半径分别为R和r,那么⑵中的猜想还成立吗?若成立,给出证明,若不成立,那么AC和AD的长与两圆半径有何关系?说明理由。
⑶ 若⊙O1、⊙O2是两个不相等的圆,半径分别为R和r,那么⑵中的猜想还成立吗?若成立,给出证明,若不成立,那么AC和AD的长与两圆半径有何关系?说明理由。






有些例题,图形的结构、问题的背景、解决的方法有类似之处,甚至有些题目就是同一题设条件,只是求证的结论的表现形式不同而已,因此进行多题一讲是很有必要的。它可以使学生感觉到很多题目可以借助于同一核心知识来解决,只要将题目的内涵与外延挖掘彻底,进而灵活运用就可以了。这样可促使学生的数学复习更有信心,不至于被大量的复习资料弄得无所适从。
例如:“相似三角形”一章中有一题:如图,在Rt△ABC中,∠ABC=Rt∠,CM 为斜边上的中线,EM⊥AB交AC于D,交BC的延长线于E,求证:CM2=DM·EM。

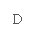





 又如,浙教版初三数学第158页14题:如图,一直线分别交△ABC的边AB,AC和BC的延长线于D、E、F,且BD=CE,求证:AC·EF=AB·DF。
又如,浙教版初三数学第158页14题:如图,一直线分别交△ABC的边AB,AC和BC的延长线于D、E、F,且BD=CE,求证:AC·EF=AB·DF。


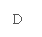



此类题很多,我将它们的同一种讲法或解法概括成几句简单易记的顺口溜:
遇等积,改等比,
横找竖找定相似。
不相似,别生气,
等线等比来代替。
这简单实用的顺口溜方法也成为学生解题时的心理调节剂,让学生享受着解题的快乐。
有些例题,简洁易证,但内涵丰富,若能深入挖掘,善加变化,往往能举一反三,达到以例代类的效果,也就是我们经常说的通过做一题达到会一类,甚至知一片的目的。这样的例题在复习中何乐而不取呢!
 例如,初三几何“两圆的公切线”中有一题:如图,⊙O1‑与⊙O2‑外切于点A,BC是⊙O1与⊙O2的公切线,B、C为切点,求证:AB⊥AC。此例简单易证,除此结论之外,可引导学生在条件不变的情况下,继续挖掘题目的内涵,得出下列结论:①根据切线长定理得:NA=NB,NA=NC,∴BN=NC,即通过A点的内公切线平分外公切线BC。②Rt△CBG-Rt△HCB∴BC2=BG·CH。即外公切线的长是两圆直径的比例中项。
例如,初三几何“两圆的公切线”中有一题:如图,⊙O1‑与⊙O2‑外切于点A,BC是⊙O1与⊙O2的公切线,B、C为切点,求证:AB⊥AC。此例简单易证,除此结论之外,可引导学生在条件不变的情况下,继续挖掘题目的内涵,得出下列结论:①根据切线长定理得:NA=NB,NA=NC,∴BN=NC,即通过A点的内公切线平分外公切线BC。②Rt△CBG-Rt△HCB∴BC2=BG·CH。即外公切线的长是两圆直径的比例中项。








在教学过程中,部分例题在经过一次讲解之后,往往被放置一边,久而久之,造成了学生轻视旧题,一味求全猎奇。从而走入题海的现象。实际上,好的例题犹如一部名著,可以一讲再讲,细细揣摩,尤其在复习阶段的教学中,将其变化延伸,拓展学生思维,于旧题中挖掘出新意,耐人寻味,留给学生的印象也深刻的多。

 例如:为复习垂径定理,出示初二几何中一道旧题:已知,如图,AB是⊙O的直径,CD是弦AE⊥CD,垂足是E,BF⊥CD,垂足是F,求证:EC=DF
例如:为复习垂径定理,出示初二几何中一道旧题:已知,如图,AB是⊙O的直径,CD是弦AE⊥CD,垂足是E,BF⊥CD,垂足是F,求证:EC=DF








 为复习初三学到的切线的性质,可将上图作新的变动:当EF变为⊙O的切线时,如图,问EN与NF是否相等?根据切线的性质定理及平行线等分线段定理,可知EN=NF
为复习初三学到的切线的性质,可将上图作新的变动:当EF变为⊙O的切线时,如图,问EN与NF是否相等?根据切线的性质定理及平行线等分线段定理,可知EN=NF






 为复习三角形相似,可将陈题再次推新,如图,可证得△ADN∽△NEB,同理△ADM∽△MEB
为复习三角形相似,可将陈题再次推新,如图,可证得△ADN∽△NEB,同理△ADM∽△MEB





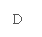

这样的陈题及题中的图形可以说是基本题和基本图,它在我们的复习教学中必能起到触类旁通,开拓思维的作用。
有些例题是为学生熟练定义、定理、法则等设计的,其目的是强化双基训练,这种题涉及的知识点相对较少,难度显得不大,但这种题往往是综合题的“垫脚石”,起导向作用。一些大题都是由一些基础题组合而成的,综合题其实是基础题的综合,因此这些基础题不可忽视,须正确对待,而今教学中对此类题有两大误区:误区一,流于形式,一带而过;误区二,事无巨细,喋喋不休,纠缠不清。为防止以上误区,正确做法是:①找出解题的突破口,点拔疏通;②看它所反映出的数学思想方法。简而言之,在对它们的讲解时,须“精讲”,将学生引导到某个知识点上即可。

 例如:“解直角三角形”中,有这样一道题,如图:△ABC中,∠A=45°,∠B=30° BC=8 求AB
例如:“解直角三角形”中,有这样一道题,如图:△ABC中,∠A=45°,∠B=30° BC=8 求AB
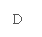


讲解此题时可以这样逐步点拔:①本题能否直接根据解直角三角形中“知二得三“来解(二、三表示直角三角形中的边、角元素);为什么?(△ABC是非直角三角形)②那如何构建直角三角形来求解本题呢?(作高)③现在该如何求解AB的长?请写清过程(另安排一学生板演)。④分析后提出一问:你对本题辅助线的添加有哪些启示?
通过以上四个层次的设计点拔,学生很快发现了此例与往例的区别,迅速找到了解决问题的途径,并顺利解题。这种易题精讲的方式,不仅避免了教师一手包办,学生生吞活剥的弊端,而且可以将学生置于主体地位,积极参与,动手动脑。
28、(2008青海西宁)某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
数学活动报告
活动小组:第一组 活动地点:学校操场
活动时间:××××年××月××日年上午9:00 活动小组组长:×××
|
课题 |
测量校内旗杆高度 |
||
|
目的 |
运用所学数学知识及数学方法解决实际问题--测量旗杆高度 |
||
|
方案 |
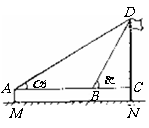 方案一 方案一 |
方案二 |
方案三 |
|
示意图 |
|
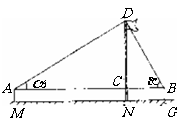 |
|
|
测量工具 |
皮尺、测角仪 |
皮尺、测角仪 |
|
|
测量数据: |
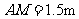 , ,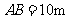 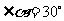 , ,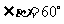 |
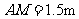 , ,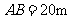 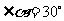 , ,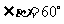 |
|
|
计算过程(结 果保留根号) |
解: |
解: |
|
|
测量结果 |
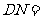 |
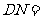 |
|
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果.
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据?长度用字母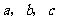 ……表示,角度用字母
……表示,角度用字母 ……表示).
……表示).
27、(2008甘肃白银)如图(1),由直角三角形边角关系,可将三角形面积公式变形,
 得
得 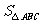 =
=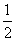 bc·sin∠A. ①
bc·sin∠A. ①
即 三角形的面积等于两边之长与夹角正弦之积的一半.
如图22(2),在⊿ABC中,CD⊥AB于D,∠ACD=α, ∠DCB=β.
∵ 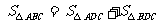 , 由公式①,得
, 由公式①,得
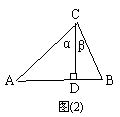
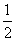 AC·BC·sin(α+β)=
AC·BC·sin(α+β)=
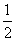 AC·CD·sinα+
AC·CD·sinα+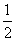 BC·CD·sinβ,
BC·CD·sinβ,
即 AC·BC·sin(α+β)= AC·CD·sinα+BC·CD·sinβ. ②
你能利用直角三角形边角关系,消去②中的AC、BC、CD吗?不能,
说明理由;能,写出解决过程.
26、(2008广东茂名)如图,某学习小组为了测量河对岸塔AB的高度,在塔底部B的正对岸点C处,测得仰角∠ACB=30°.
(1)若河宽BC是60米,求塔AB的高(结果精确到0.1米);(4分)
(参考数据: ≈1.414,
≈1.414,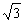 ≈1.732)
≈1.732)
(2)若河宽BC的长度无法度量,如何测量塔AB的高度呢?小明想出了另外一种方法:从点C出发,沿河岸CD的方向(点B、C、D在同一平面内,且CD⊥BC)走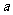 米,到达D处,测得∠BDC=60°,这样就可以求得塔AB的高度了.请你用这种方法求出塔AB的高.
米,到达D处,测得∠BDC=60°,这样就可以求得塔AB的高度了.请你用这种方法求出塔AB的高.
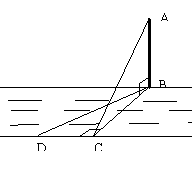
25、(2008湖南怀化)某校教学楼后面紧邻一个土坡,坡上面是一块平地,如图12所示,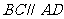 ,斜坡
,斜坡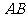 长
长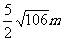 ,坡度
,坡度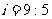 .为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,地质人员勘测,当坡角不超过
.为了防止山体滑坡,保障安全,学校决定对该土坡进行改造,地质人员勘测,当坡角不超过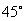 时,可确保山体不滑坡.
时,可确保山体不滑坡.
(1)求改造前坡B到地面的垂直距离 的长;
的长;
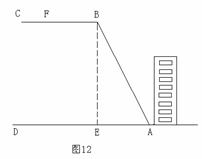 (2)为确保安全,学校计划改造时保持坡脚
(2)为确保安全,学校计划改造时保持坡脚 不动,坡顶
不动,坡顶 沿
沿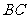 削进到
削进到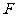 处,问
处,问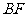 至少是多少米?
至少是多少米?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com