
(二)填空题:
1.在Rt△ABC中,∠C=Rt∠,AC=3,BC=4,则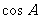 =_____.
=_____.
2.若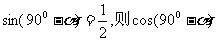 =_____.
=_____.
3.在Rt△ABC中,∠C=90°,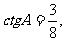 b=6,则c=_____.
b=6,则c=_____.
4.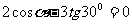 ,则锐角
,则锐角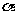 =_____度.
=_____度.
5.在RtΔABC中,∠C=90°,AD平分∠BAC,若AC=12,AD=8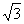 ,则BC=_____.
,则BC=_____.
6.函数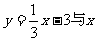 轴的交点A的坐标是_____,与
轴的交点A的坐标是_____,与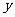 轴的交点B的坐标是_____,S△AOB=_____.
轴的交点B的坐标是_____,S△AOB=_____.
7.在Rt△ABC中,∠C=90°,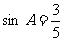 ,斜边c=10,则Rt△ABC内切圆的半径是_____,内心与外心间的距离是_____.
,斜边c=10,则Rt△ABC内切圆的半径是_____,内心与外心间的距离是_____.
8.函数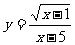 的自变量
的自变量 的取值范围是_____.
的取值范围是_____.
9.抛物线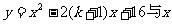 轴只有一个交点,则
轴只有一个交点,则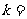 _____.
_____.
10.抛物线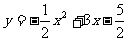 的顶点关于
的顶点关于 轴的对称点的坐标是_____.
轴的对称点的坐标是_____.
11.一次函数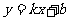 的图象经过(2,2)和(3,5)点,则函数解析式是_____.
的图象经过(2,2)和(3,5)点,则函数解析式是_____.
12.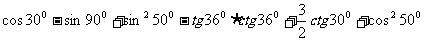 的值是_____.
的值是_____.
13.如果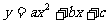 的图象经过(1,4),(0,2)和(-2,-8)三点,则
的图象经过(1,4),(0,2)和(-2,-8)三点,则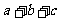 的值是_____.
的值是_____.
14.已知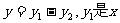 的正比例函数,
的正比例函数,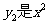 的反比例函数,且
的反比例函数,且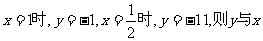 间的函数解析式是_____.
间的函数解析式是_____.
15.已知直线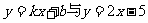 交点的横坐标是1,与
交点的横坐标是1,与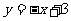 交点的纵坐标是4,则函数
交点的纵坐标是4,则函数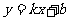 的解析式是_____.
的解析式是_____.
16.已知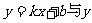 轴交点的纵坐标是2,它与两坐标围成的三角形的面积是7,则这个函数的解析式是_____.
轴交点的纵坐标是2,它与两坐标围成的三角形的面积是7,则这个函数的解析式是_____.
17.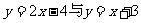 相交点C,设两直线与
相交点C,设两直线与 轴分别交于A,B,与
轴分别交于A,B,与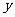 轴交于P,Q,则点C的坐标是_____.S△ABC=_____,S△CPQ=_____.
轴交于P,Q,则点C的坐标是_____.S△ABC=_____,S△CPQ=_____.
18.直线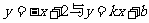 的交点坐标是C(3,-1),两直线与
的交点坐标是C(3,-1),两直线与 轴分别交A,B,且S△ABC=9,则直线的解析式是_____.
轴分别交A,B,且S△ABC=9,则直线的解析式是_____.
19.二次函数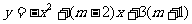 的图象与
的图象与 轴交于A,B两点,(A在B的左边)与
轴交于A,B两点,(A在B的左边)与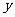 轴交于C,线段OA与OB的长的积等于6,(O是坐标原点),则m的值是_____,S△ABC=_____.
轴交于C,线段OA与OB的长的积等于6,(O是坐标原点),则m的值是_____,S△ABC=_____.
(一)判断题
1.一次函数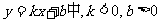 ,则它的图象经过一,二,四象限( )
,则它的图象经过一,二,四象限( )
2.当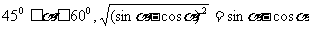 ( )
( )
3.已知斜坡AB的坡度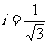 ,则坡角
,则坡角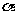 的度数是60°( )
的度数是60°( )
4.函数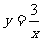 的图象的两支在第一,三象限,
的图象的两支在第一,三象限,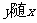 的增大而增大( )
的增大而增大( )
5.已知点A(-4,3)和(-4,-3),则A,B关于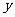 轴对称( )
轴对称( )
6.在Rt△ABC中,AD是斜边BC边上的高,若BC=6,DC=2,则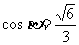 ( )
( )
6.用待定系数法确定函数解析式是较难的.要总结经验归纳类型.
5.特别要注意:一次函数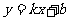 和二次函数
和二次函数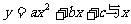 轴交点的坐标的求法,即点在
轴交点的坐标的求法,即点在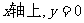 ,此时
,此时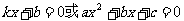 ,它们与
,它们与 轴交点的纵坐标都为零,而横坐标是上述方程的根.二次函数
轴交点的纵坐标都为零,而横坐标是上述方程的根.二次函数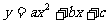 中的
中的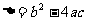 的值,决定着抛物线
的值,决定着抛物线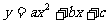 与
与 轴交点的个数.
轴交点的个数. 时有两个交点;
时有两个交点; 时只有一个交点;
时只有一个交点; 时没有交点。会利用
时没有交点。会利用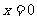 求
求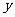 ,并得出图象与
,并得出图象与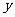 轴的交点的坐标.
轴的交点的坐标.
4.要注意结合图象理解:正比例函数、反比例函数、一次函数和二次函数的性质,要理解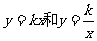 中的
中的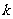 的正、负,知道图象在第几象限,
的正、负,知道图象在第几象限,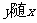 的增大而增大还是减小.在
的增大而增大还是减小.在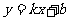 中,要由
中,要由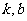 的符号画出图象草图.知道
的符号画出图象草图.知道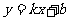 的图象的位置,反之由
的图象的位置,反之由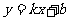 在坐标系中的位置确定
在坐标系中的位置确定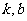 的符号,在二次函数
的符号,在二次函数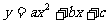 中知道
中知道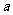 的正、负确定开口方向,
的正、负确定开口方向,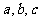 的正、负,确定抛物线在坐标系中的大体位置.
的正、负,确定抛物线在坐标系中的大体位置.
3.在直角坐标系中,某个点的横坐标是该点向 轴做垂线,垂足在
轴做垂线,垂足在 轴所表示的那个实数,纵坐标是该点向
轴所表示的那个实数,纵坐标是该点向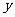 轴作垂线,垂足在
轴作垂线,垂足在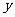 轴上表示的实数.点在
轴上表示的实数.点在 轴上,纵坐标为0,即(
轴上,纵坐标为0,即( ,0).点在
,0).点在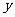 轴上,横坐标为0,即(0,
轴上,横坐标为0,即(0,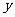 ).若两点关于
).若两点关于 轴对称, 则横坐标相同,纵坐标互为相反数. 若两点关于
轴对称, 则横坐标相同,纵坐标互为相反数. 若两点关于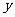 轴对称, 则纵坐标相同,横坐标互为相反. 若两点关于原点对称,则横坐标、纵坐标都互为相反数.
轴对称, 则纵坐标相同,横坐标互为相反. 若两点关于原点对称,则横坐标、纵坐标都互为相反数.
2.正弦、正切函数都是增函数。即当角度在00-- 900间变化时,正弦、正切值随着角度的增大而增大。如:化简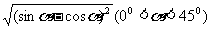 ,我们先将此式由性质化简
,我们先将此式由性质化简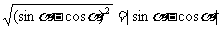 ,然后看是
,然后看是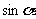 大还是
大还是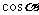 大.不妨在
大.不妨在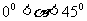 中取
中取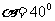 ,则
,则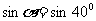 ,
,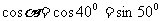 (化成同名三角函数)∵
(化成同名三角函数)∵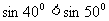 ,∴
,∴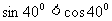 ,这说明
,这说明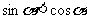 ,
,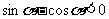 .∴
.∴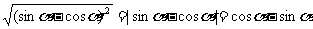 (负数的绝对值是其相反数)。再如:已知
(负数的绝对值是其相反数)。再如:已知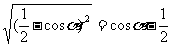 ,确定角
,确定角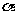 的取值范围。∵
的取值范围。∵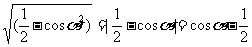 ,∴
,∴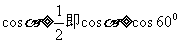 ,因为余弦函数是随着角度的增大余弦值反而越小,∴
,因为余弦函数是随着角度的增大余弦值反而越小,∴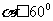 .
.
1.利用直角三角形边角之间的关系来解直角三角形,最主要的是记住定义。譬如说,我们要求直角三角形中一个锐角的度数,需根据已知条件是这个角的哪些边来选择函数定义,若已知直角三边形的一个锐角和一边长求另一边长也是如此.
(二)1.了解平面直角坐标系的有关概念,会由点的位置确定点的坐标,会由点的 坐标确定点的位置.
2.理解函数的意义,能根据一个具体的函数解析式,确定自变量的取值范围, 并会由自变量的值求出函数值.
3.掌握正比例函数、反比例函数、一次函数、二次函数的概念及性质,会画出 图象.
4.能根据不同条件,用待定系数法求函数解析式.
(一)1.理解锐角三角函数定义,会用锐角三角形定义列出函数关系式解直角三角形.
2.了解锐角三角函数的四个同角间的函数恒等式,并会解一些相关的题目.
3.理解锐角三角函数的性质,会比较在某个范围内正弦和正弦,正弦和余弦, 正切和正切,正切和余切的大小,及利用函数值的大小判断角的大小.
4.熟记特殊角的三角函数组,并会准确的计算.
5.会用解直角三角形的有关知识,解某些实际问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com