
例如:如图4-1:AD为△ABC的中线,且∠1=∠2,∠3=∠4,求证:BE+CF>EF
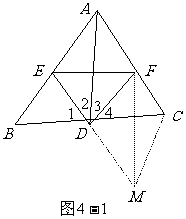 证明:延长ED至M,使DM=DE,连接
证明:延长ED至M,使DM=DE,连接
CM,MF。在△BDE和△CDM中,
∵
∴△BDE≌△CDM (SAS)
又∵∠1=∠2,∠3=∠4 (已知)
∠1+∠2+∠3+∠4=180°(平角的定义)
∴∠3+∠2=90°
即:∠EDF=90°
∴∠FDM=∠EDF =90°
在△EDF和△MDF中
∵
∴△EDF≌△MDF (SAS)
∴EF=MF (全等三角形对应边相等)
∵在△CMF中,CF+CM>MF(三角形两边之和大于第三边)
∴BE+CF>EF
注:上题也可加倍FD,证法同上。
注意:当涉及到有以线段中点为端点的线段时,可通过延长加倍此线段,构造全等三角形,使题中分散的条件集中。
例如:如图3-1:已知AD为△ABC的中线,且∠1=∠2,∠3=∠4,求证:BE+CF>EF。
 分析:要证BE+CF>EF ,可利用三角形三边关系定理证明,须把BE,CF,EF移到同一个三角形中,而由已知∠1=∠2,∠3=∠4,可在角的两边截取相等的线段,利用三角形全等对应边相等,把EN,FN,EF移到同一个三角形中。
分析:要证BE+CF>EF ,可利用三角形三边关系定理证明,须把BE,CF,EF移到同一个三角形中,而由已知∠1=∠2,∠3=∠4,可在角的两边截取相等的线段,利用三角形全等对应边相等,把EN,FN,EF移到同一个三角形中。
证明:在DA上截取DN=DB,连接NE,NF,则DN=DC,
在△DBE和△DNE中:
∵
∴△DBE≌△DNE (SAS)
∴BE=NE(全等三角形对应边相等)
同理可得:CF=NF
在△EFN中EN+FN>EF(三角形两边之和大于第三边)
∴BE+CF>EF。
注意:当证题有角平分线时,常可考虑在角的两边截取相等的线段,构造全等三角形,然后用全等三角形的性质得到对应元素相等。
例如:如图2-1:已知D为△ABC内的任一点,求证:∠BDC>∠BAC。
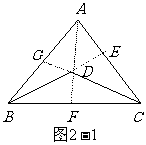 分析:因为∠BDC与∠BAC不在同一个三角形中,没有直接的联系,可适当添加辅助线构造新的三角形,使∠BDC处于在外角的位置,∠BAC处于在内角的位置;
分析:因为∠BDC与∠BAC不在同一个三角形中,没有直接的联系,可适当添加辅助线构造新的三角形,使∠BDC处于在外角的位置,∠BAC处于在内角的位置;
证法一:延长BD交AC于点E,这时∠BDC是△EDC的外角,
∴∠BDC>∠DEC,同理∠DEC>∠BAC,∴∠BDC>∠BAC
证法二:连接AD,并延长交BC于F
∵∠BDF是△ABD的外角
∴∠BDF>∠BAD,同理,∠CDF>∠CAD
∴∠BDF+∠CDF>∠BAD+∠CAD
即:∠BDC>∠BAC。
注意:利用三角形外角定理证明不等关系时,通常将大角放在某三角形的外角位置上,小角放在这个三角形的内角位置上,再利用不等式性质证明。
例1:已知如图1-1:D、E为△ABC内两点,求证:AB+AC>BD+DE+CE.
证明:(法一)将DE两边延长分别交AB、AC 于M、N,
在△AMN中,AM+AN > MD+DE+NE;(1)
在△BDM中,MB+MD>BD; (2)
在△CEN中,CN+NE>CE; (3)
由(1)+(2)+(3)得:
AM+AN+MB+MD+CN+NE>MD+DE+NE+BD+CE
∴AB+AC>BD+DE+EC
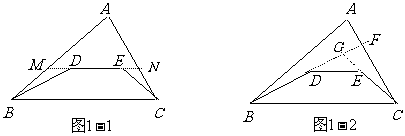
(法二:)如图1-2, 延长BD交 AC于F,延长CE交BF于G,
在△ABF和△GFC和△GDE中有:
AB+AF> BD+DG+GF (三角形两边之和大于第三边)(1)
GF+FC>GE+CE(同上)………………………………(2)
DG+GE>DE(同上)……………………………………(3)
由(1)+(2)+(3)得:
AB+AF+GF+FC+DG+GE>BD+DG+GF+GE+CE+DE
∴AB+AC>BD+DE+EC。
(四)①由

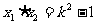 得
得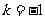
②∵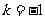 ∴
∴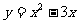 与
与 轴交于A(0,0)和B(3,0)
轴交于A(0,0)和B(3,0)
设存在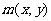
由题意得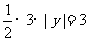
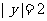
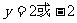
将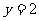 舍去(若
舍去(若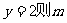 点必在
点必在 轴上方,此时△AB
轴上方,此时△AB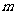 是钝角三角形,与△A
是钝角三角形,与△A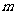 B是锐角三角形不符)
B是锐角三角形不符)
当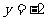 时,
时, 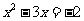
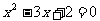
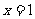
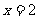
∴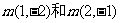
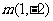 也会在[因为
也会在[因为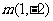 ]在对称轴左边.
]在对称轴左边.
∴适合条件的点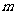 是(2,-2)
是(2,-2)
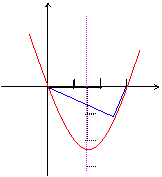 y
y 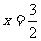
A B
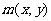
(三)1.D 2.C 3.C
(二)1. 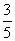 2.
2. 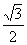 3.
3. 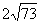 4. 30° 5.
4. 30° 5. 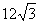 6. (9,0),(0,-3)
6. (9,0),(0,-3) 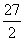
7. 2; 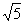 8.
8. 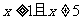 9. ¨5或3 10. (3,-2) 11.
9. ¨5或3 10. (3,-2) 11. 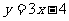
12.
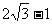 13. 4 14.
13. 4 14. 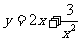 15.
15.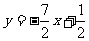
16.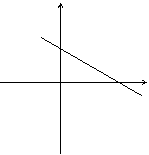 提示:设
提示:设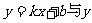 轴交于(0,2)
y
轴交于(0,2)
y
它与 轴交于(
轴交于(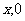 ),则S△AOB=
),则S△AOB=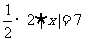 A(0,2)
A(0,2)

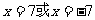
∴与 轴交于(7,0)和(-7,0) 0 B(
轴交于(7,0)和(-7,0) 0 B(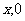 ) x
) x
将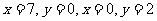 代入公式
代入公式 ,
,
将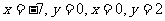 代入得
代入得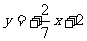
17.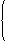
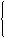 交点C的坐标是
交点C的坐标是 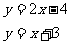 的解
的解 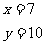 S△ABC=25 S△CPQ=
S△ABC=25 S△CPQ=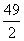
18.提示: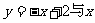 轴交于(2,0),
轴交于(2,0),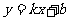 与
与 轴交于(
轴交于(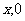 )
)
则
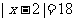
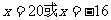
∴B(20,0)或(-16,0)分别和C(3,-1)代入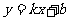 得
得
 ∴
∴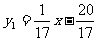 和
和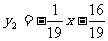 y
y
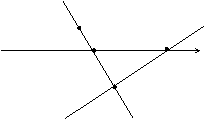
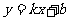
0
A(2,0) B( ,0)
,0)
C(3,-1)
19. 二次函数
二次函数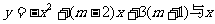 轴交于A(
轴交于A(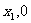 )和B(
)和B(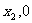 ),
),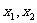 是
是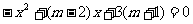 的根.线段OA的长是
的根.线段OA的长是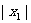 ,线段OB的长是
,线段OB的长是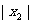 ,由题意得:
,由题意得: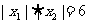 ,若图象是
,若图象是
A(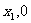 ) B(
) B(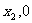 )
)
则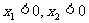

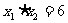 两根之积是6
两根之积是6
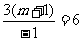
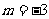
 若图象是
若图象是
A(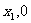 ) B(
) B(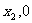 )
)
则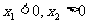
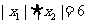

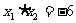

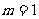
∴ S△ABC=3或15
S△ABC=3或15
(一)1.√ 2.√ 3.× 4.× 5.× 6.√
(四)解答题
已知关于 的二次函数
的二次函数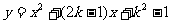 ,求:
,求:
1.关于 的一元二次方程
的一元二次方程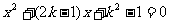 的两根平方和等于9,求
的两根平方和等于9,求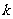 的值.
的值.
2.在1的条件下,设这个二次函数的图象与 轴从左到右交于A,B两点,问在对称轴的右边的图象上,是否存在点M,使锐角△AMB的面积等于3,若存在,请写出点M的坐标;若不存在,请说明理由.
轴从左到右交于A,B两点,问在对称轴的右边的图象上,是否存在点M,使锐角△AMB的面积等于3,若存在,请写出点M的坐标;若不存在,请说明理由.
(三)选择题:
1.若函数 在同一坐标系中相交,且
在同一坐标系中相交,且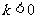 ,则交点在:
,则交点在:
A.第一象限 B.第二象限 C.第二,四象限 D.第四象限
2.∠A是锐角,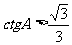 ,则∠A:
,则∠A:
A.<30° B.> 30° C.<60° D.>60°
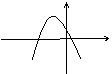
3.在同一坐标系中,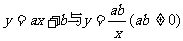 的图象大致是:
的图象大致是:
y y y y

0 0 0 0
x x x x
A. B. C. D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com