
2、 用三角板拼角
例4用一副三角板可以拼成小于平角的角 个。
分析:一副三角板中共有30°、45°、60°、90°四种角度,所以可以拼成30°、45°、60°、90°、75°、120°、105°、135°、150°、15°十个角。
解:用一副三角板可以拼成十个小于平角的角。
例5把一副三角板的直角顶点O重叠在一起,
1)如图4,当OB平分∠COD时,则∠AOD和∠BOC的和是多少度?
2)如图5,当OB不平分∠COD时,则∠AOD和∠BOC的和是多少度?
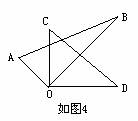
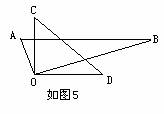
分析:本题渗透着由特殊到一般认识事物规律的思想。通过图4的特殊条件,探求出结论,再通过图5,把结论推广到一般情形。
解:1)∵OB平分∠COD∴∠COB=∠BOD=45°∴∠COA=90°-45°=45°∴∠AOD+∠BOC=∠AOC+∠COD+∠BOC=45°+90°+45°=180°
2)∵∠AOC+∠BOC=90°∠BOD+∠BOC=90°∴∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC∴∠AOD+∠BOC=(∠AOC+∠BOC)+(∠BOD+∠BOC)=90°+90°=180°
1、 用三角板拼多边形
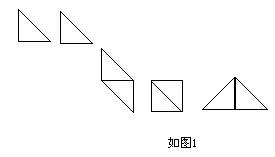 例1用两块完全重合的等腰直角三角板,拼成下列图形:
例1用两块完全重合的等腰直角三角板,拼成下列图形:
①平行四边形(一般平行四边形)②矩形(不包含正方形)③正方形④等边三角形⑤等腰直角三角形,一定能拼成的图形是: :
A)①②③ B)①③⑤ C)②③⑤ D)①③④⑤
分析:如图1,所示,可知两块完全重合的等腰直角三角板能拼成一般平行四边形、正方形、和等腰直角三角形。
解:选(B)。
例2 用含30°的两个直角三角板,能拼成不同形状的平行四边形的个数为 :
A)1个 B)2个 C)3个 D)4个
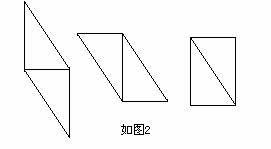 分析:如图2,所示,用含30°的两个直角三角板,能拼成不同形状的平行四边形为两个一般平行四边形和一个矩形。
分析:如图2,所示,用含30°的两个直角三角板,能拼成不同形状的平行四边形为两个一般平行四边形和一个矩形。
解:选(C)
例3 用含30°的两个直角三角板,能拼成不同形状的四边形的个数为 :
A)1个 B)2个 C)3个 D)4个
 分析:如图3,用含30°的两个直角三角板,能拼成不同形状的四边形的为两个一般平行四边形,一个矩形和一个凸四边形。
分析:如图3,用含30°的两个直角三角板,能拼成不同形状的四边形的为两个一般平行四边形,一个矩形和一个凸四边形。
解:选(D)
2. 如图6,AD:DB=1:3,AE:EC=3:1,求BF:FC。
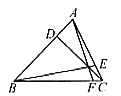
答案:1. 1:10;2. 9:1
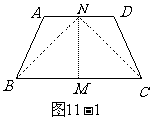
例如:如图11-1:AB=DC,∠A=∠D 求证:∠ABC=∠DCB。
分析:由AB=DC,∠A=∠D,想到如取AD的中点N,连接NB,NC,再由SAS公理有△ABN≌△DCN,故BN=CN,∠ABN=∠DCN。下面只需证∠NBC=∠NCB,再取BC的中点M,连接MN,则由SSS公理有△NBM≌△NCM,所以∠NBC=∠NCB。问题得证。
证明:取AD,BC的中点N、M,连接NB,NM,NC。则AN=DN,BM=CM,在△ABN和△DCN中 ∵  ∴△ABN≌△DCN (SAS)
∴△ABN≌△DCN (SAS)
∴∠ABN=∠DCN NB=NC (全等三角形对应边、角相等)
 在△NBM与△NCM中
在△NBM与△NCM中
∵
∴△NMB≌△NCM,(SSS) ∴∠NBC=∠NCB (全等三角形对应角相等)∴∠NBC+∠ABN =∠NCB+∠DCN
即∠ABC=∠DCB。
巧求三角形中线段的比值
例1. 如图1,在△ABC中,BD:DC=1:3,AE:ED=2:3,求AF:FC。
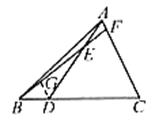
解:过点D作DG//AC,交BF于点G 所以DG:FC=BD:BC
因为BD:DC=1:3 所以BD:BC=1:4 即DG:FC=1:4,FC=4DG
因为DG:AF=DE:AE 又因为AE:ED=2:3 所以DG:AF=3:2
即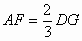 所以AF:FC=
所以AF:FC=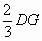 :4DG=1:6
:4DG=1:6
例2. 如图2,BC=CD,AF=FC,求EF:FD
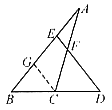 解:过点C作CG//DE交AB于点G,则有EF:GC=AF:AC
解:过点C作CG//DE交AB于点G,则有EF:GC=AF:AC
因为AF=FC 所以AF:AC=1:2 即EF:GC=1:2
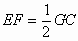 因为CG:DE=BC:BD 又因为BC=CD
因为CG:DE=BC:BD 又因为BC=CD
所以BC:BD=1:2 CG:DE=1:2 即DE=2GC
因为FD=ED-EF=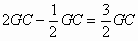 所以EF:FD=
所以EF:FD=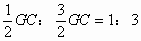
小结:以上两例中,辅助线都作在了“已知”条件中出现的两条已知线段的交点处,且所作的辅助线与结论中出现的线段平行。请再看两例,让我们感受其中的奥妙!
例3. 如图3,BD:DC=1:3,AE:EB=2:3,求AF:FD。
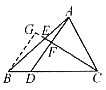
解:过点B作BG//AD,交CE延长线于点G。 所以DF:BG=CD:CB
因为BD:DC=1:3 所以CD:CB=3:4 即DF:BG=3:4
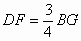 因为AF:BG=AE:EB
又因为AE:EB=2:3
因为AF:BG=AE:EB
又因为AE:EB=2:3
所以AF:BG=2:3
即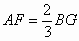
所以AF:DF=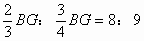
例4. 如图4,BD:DC=1:3,AF=FD,求EF:FC。
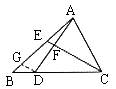
图4
解:过点D作DG//CE,交AB于点G
所以EF:DG=AF:AD
因为AF=FD 所以AF:AD=1:2
即EF:DG=1:2
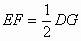
因为DG:CE=BD:BC
又因为BD:CD=1:3
所以BD:BC=1:4
即DG:CE=1:4
CE=4DG
因为FC=CE-EF=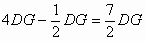
所以EF:FC=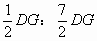 =1:7
=1:7
练习:
1. 如图5,BD=DC,AE:ED=1:5,求AF:FB。
例如:已知:如图10-1;AC、BD相交于O点,且AB=DC,AC=BD,求证:∠A=∠D。
分析:要证∠A=∠D,可证它们所在的三角形△ABO和△DCO全等,而只有AB=DC和对顶角两个条件,差一个条件,,难以证其全等,只有另寻其它的三角形全等,由AB=DC,AC=BD,若连接BC,则△ABC和△DCB全等,所以,证得∠A=∠D。
 证明:连接BC,在△ABC和△DCB中
证明:连接BC,在△ABC和△DCB中
∵

∴△ABC≌△DCB (SSS)
∴∠A=∠D (全等三角形对应边相等)
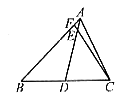
 例如:如图9-1:在Rt△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD的延长于E 。求证:BD=2CE
例如:如图9-1:在Rt△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD的延长于E 。求证:BD=2CE
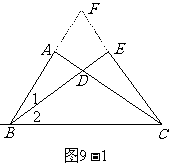 分析:要证BD=2CE,想到要构造线段2CE,同时CE与∠ABC的平分线垂直,想到
要将其延长。
分析:要证BD=2CE,想到要构造线段2CE,同时CE与∠ABC的平分线垂直,想到
要将其延长。
证明:分别延长BA,CE交于点F。
∵BE⊥CF (已知)
∴∠BEF=∠BEC=90° (垂直的定义)
在△BEF与△BEC中,
∵ 
∴△BEF≌△BEC(ASA)∴CE=FE=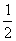 CF (全等三角形对应边相等)
CF (全等三角形对应边相等)
∵∠BAC=90° BE⊥CF (已知)
∴∠BAC=∠CAF=90° ∠1+∠BDA=90°∠1+∠BFC=90°
∴∠BDA=∠BFC
在△ABD与△ACF中

∴△ABD≌△ACF (AAS)∴BD=CF (全等三角形对应边相等) ∴BD=2CE
例如:如图8-1:AB∥CD,AD∥BC 求证:AB=CD。
分析:图为四边形,我们只学了三角形的有关知识,必须把它转化为三角形来解决。
证明:连接AC(或BD)
∵AB∥CD AD∥BC (已知)
∴∠1=∠2,∠3=∠4 (两直线平行,内错角相等)
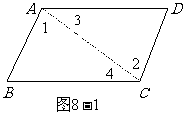 在△ABC与△CDA中
在△ABC与△CDA中
∵ 
∴△ABC≌△CDA (ASA)
∴AB=CD(全等三角形对应边相等)
例如:如图7-1:已知AC=BD,AD⊥AC于A ,BC⊥BD于B, 求证:AD=BC
分析:欲证 AD=BC,先证分别含有AD,BC的三角形全等,有几种方案:△ADC与△BCD,△AOD与△BOC,△ABD与△BAC,但根据现有条件,均无法证全等,差角的相等,因此可设法作出新的角,且让此角作为两个三角形的公共角。
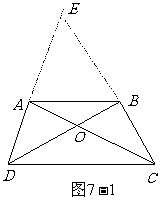 证明:分别延长DA,CB,它们的延长交于E点,
证明:分别延长DA,CB,它们的延长交于E点,
∵AD⊥AC BC⊥BD (已知)
∴∠CAE=∠DBE =90° (垂直的定义)
在△DBE与△CAE中
∵
∴△DBE≌△CAE (AAS)
∴ED=EC EB=EA (全等三角形对应边相等)
∴ED-EA=EC-EB
即:AD=BC。
(当条件不足时,可通过添加辅助线得出新的条件,为证题创造条件。)
例如:已知如图6-1:在△ABC中,AB>AC,∠1=∠2,P为AD上任一点。
求证:AB-AC>PB-PC。
分析:要证:AB-AC>PB-PC,想到利用三角形三边关系定理证之,因为欲证的是线段之差,故用两边之差小于第三边,从而想到构造第三边AB-AC,故可在AB上截取AN等于AC,得AB-AC=BN, 再连接PN,则PC=PN,又在△PNB中,PB-PN<BN,
即:AB-AC>PB-PC。
证明:(截长法)
在AB上截取AN=AC连接PN , 在△APN和△APC中
∵
∴△APN≌△APC (SAS)
∴PC=PN (全等三角形对应边相等)
∵在△BPN中,有 PB-PN<BN (三角形两边之差小于第三边)
∴BP-PC<AB-AC
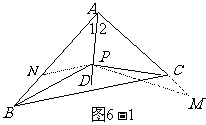 证明:(补短法) 延长AC至M,使AM=AB,连接PM,
证明:(补短法) 延长AC至M,使AM=AB,连接PM,
在△ABP和△AMP中
∵ 
∴△ABP≌△AMP (SAS)
∴PB=PM (全等三角形对应边相等)
又∵在△PCM中有:CM>PM-PC(三角形两边之差小于第三边)
∴AB-AC>PB-PC。
例如:如图5-1:AD为 △ABC的中线,求证:AB+AC>2AD。
分析:要证AB+AC>2AD,由图想到: AB+BD>AD,AC+CD>AD,所以有AB+AC+ BD+CD>AD+AD=2AD,左边比要证结论多BD+CD,故不能直接证出此题,而由2AD想到要构造2AD,即加倍中线,把所要证的线段转移到同一个三角形中去。
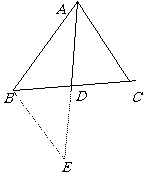 证明:延长AD至E,使DE=AD,连接BE,则AE=2AD
证明:延长AD至E,使DE=AD,连接BE,则AE=2AD
∵AD为△ABC的中线 (已知)
∴BD=CD (中线定义)
在△ACD和△EBD中

∴△ACD≌△EBD (SAS)
∴BE=CA(全等三角形对应边相等)
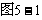 ∵在△ABE中有:AB+BE>AE(三角形两边之和大于第三边)
∵在△ABE中有:AB+BE>AE(三角形两边之和大于第三边)
∴AB+AC>2AD。
(常延长中线加倍,构造全等三角形)
练习:已知△ABC,AD是BC边上的中线,分别以AB边、AC边为直角边各向形外作等腰直角三角形,如图5-2, 求证EF=2AD。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com