
7、若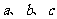 在数轴上的对应点如图所示,
在数轴上的对应点如图所示,
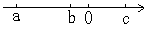
化简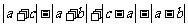
6、已知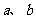 互为相反数,
互为相反数,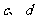 互为倒数,
互为倒数,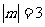 ,求
,求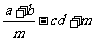
5、倒数等于本身的数是_________;绝对值等于本身的数是_________;
相反数等于本身的数是_________;平方等于本身的数是_________;
立方等于本身的数是_________;
4、当a <0时,化简 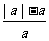 得( ).
得( ).
A、–2 B、0 C、1 D、2
3、如图所示,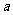 、
、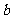 、
、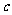 表示有理数,则
表示有理数,则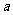 、
、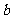 、
、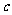 的大小顺序是( )
的大小顺序是( )
A、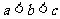 B、
B、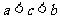 C、
C、 D、
D、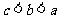
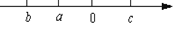
2、数轴上表示下列各数: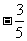 ,0,1.5,-6,2,
,0,1.5,-6,2,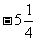

1、把下列各数填在相应的集合中:
8,-1,-0.4,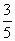 ,0,-
,0,-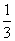 ,6.9,-
,6.9,- ,
,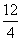 ,-300%
,-300%
正数集合:{ };负数集合:{ };
整数集合:{ };分数集合:{ };
5、 用三角板拼图证明勾股定理
例9今有四块完全相同的直角三角板,两条直角边的长分别为a、b,斜边的长为c。请利用这四块直角三角板拼成一个图形,并利用拼成的图形证明勾股定理。
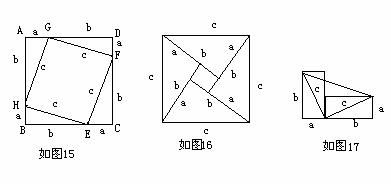
分析:本题主要考查学生动手拼图能力和图形的面积求解。
解:拼图如图15、如图16、如图17所示。下面以图15为例给出一种证明。
易证,四边形ABCD、四边形EFGH都是正方形,所以
所以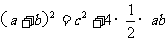 ,所以
,所以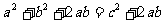 即
即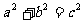 (证毕)
(证毕)
4、 滑动三角板
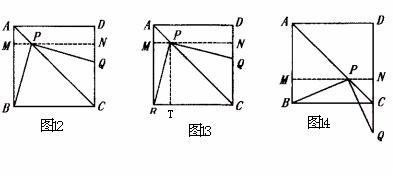
例8 操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.
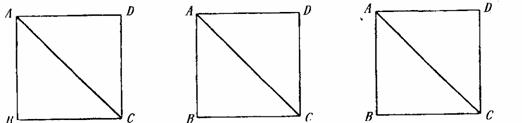
图9??????????图10???????????图11
探究:设A、P两点间的距离为x.
(1)当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到结论;
(2)当点Q在边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式,并写出自变量x的取值范围;
(3)当点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由.
(图9、图10、图11的形状大小相同,图9供操作、实验用,图10和图11备用)
分析:这是一道考查学生数学综合素质的好题。
(1)解:PQ=PB
证明如下:过点P作MN∥BC,分别交AB于点M,交CD于点N,那么四边形AMND和四边形BCNM都是矩形,△AMP和△CNP都是等腰直角三角形(如图12).
∴ NP=NC=MB.∵ ∠BPQ=90°,∴ ∠QPN+∠BPM=90°.
而∠BPM+∠PBM=90°,∴ ∠QPN=∠PBM.
又∵ ∠QNP=∠PMB=90°,∴ △QNP≌△PMB.
∴ PQ=PB.
(2)解法一
由(1)△QNP≌△PMB.得NQ=MP.
∵ AP=x,∴ AM=MP=NQ=DN=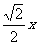 ,BM=PN=CN=1-
,BM=PN=CN=1-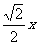 ,
,
∴ CQ=CD-DQ=1-2·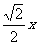 =1-
=1-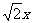 .
.
得S△PBC=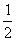 BC·BM=
BC·BM=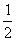 ×1×(1-
×1×(1-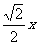 )=
)=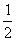 -
- x.
x.
S△PCQ=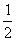 CQ·PN=
CQ·PN=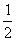 ×(1-
×(1-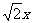 )(1-
)(1-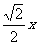 )=
)=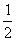 -
- +
+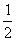 x2
x2
S四边形PBCQ=S△PBC+S△PCQ=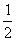 x2-
x2-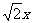 +1.即 y=
+1.即 y=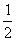 x2-
x2-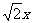 +1(0≤x<
+1(0≤x<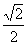 ).
).
解法二
作PT⊥BC,T为垂足(如图13),那么四边形PTCN为正方形.
∴ PT=CB=PN.
又∠PNQ=∠PTB=90°,PB=PQ,∴△PBT≌△PQN.
S四边形PBCQ=S△四边形PBT+S四边形PTCQ=S四边形PTCQ+S△PQN=S正方形PTCN ?
=CN2=(1-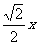 )2=
)2=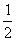 x2-
x2-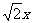 +1
+1
∴ y=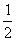 x2-
x2-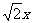 +1(0≤x<
+1(0≤x<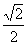 ).
).
(3)△PCQ可能成为等腰三角形
①当点P与点A重合,点Q与点D重合,这时PQ=QC,△PCQ是等腰三角形,
此时x=0
②当点Q在边DC的延长线上,且CP=CQ时,△PCQ是等腰三角形(如图14)
解法一 此时,QN=PM=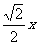 ,CP=
,CP=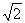 -x,CN=
-x,CN=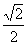 CP=1-
CP=1-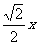 .
.
∴ CQ=QN-CN=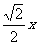 -(1-
-(1-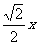 )=
)=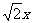 -1.
-1.
当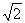 -x=
-x=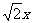 -1时,得x=1.
-1时,得x=1.
解法二 此时∠CPQ=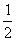 ∠PCN=22.5°,∠APB=90°-22.5°=67.5°,
∠PCN=22.5°,∠APB=90°-22.5°=67.5°,
∠ABP=180°-(45°+67.5°)=67.5°,得∠APB=∠ABP,
∴ AP=AB=1,∴ x=1.
3、旋转三角板
 例6如图6,三角板ABC中,AC=b,∠C=90°,将三角板ABC饶C点顺时针旋转90°,那么点A移动所经过的路线是 。(不取近似值)
例6如图6,三角板ABC中,AC=b,∠C=90°,将三角板ABC饶C点顺时针旋转90°,那么点A移动所经过的路线是 。(不取近似值)
分析:三角板ABC饶C点顺时针旋转90°,边CA转到水平位置,点A所经过的路线为以C为圆心,以CA为半径,且圆心角为90的扇形的弧长。
解:A移动所经过的路线=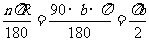
例7 把两个全等的等腰直角三角形ABC和EFG(其直角边长均为4)叠放在一起,如图7,且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合.现将三角板EFG绕O点顺时针旋转α(旋转角α满足条件:0°<α<90°),四边形CHGK是旋转过程中两三角板的重叠部分(如图8).
(1)在上述旋转过程中,BH与CH有怎样的数量关系?四边形BHGK的面积有何变化?证明你发现的结论;
(2)连接HK,在上述旋转过程中,设BH=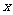 ,△GKH的面积为
,△GKH的面积为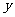 ,求
,求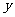 与
与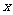 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量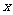 的取值范围;
的取值范围;
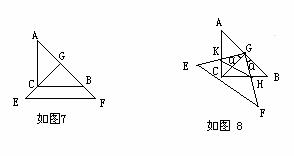 (3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的
(3)在(2)的前提下,是否存在某一位置,使△GKH的面积恰好等于△ABC面积的 ?若存在,求出此时
?若存在,求出此时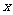 的值;若不存在,说明理由.
的值;若不存在,说明理由.
分析:这是一道集旋转、探索、证明为一体的好题。
解:(1)在上述旋转过程中,BH=CK,四边形CHGK的面积不变,是一个定值,且为三角形ABC面积的一半。
证明:连结CG
∵△ABC为等腰直角三角形,O(G)为其斜边中点
∴CG=BG,CG⊥AB.
∴∠ACG=∠B=45°.
∵∠BGH与∠CGK均为旋转角,
∴∠BGH=∠CGK.
∴△BGH≌△CGK.
∴BH=CK,S△BGH=S△CGK.
∴S四边形CHGK=S△CHG+S△CGK=S△CHG+S△BGH=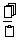 S△ABC=
S△ABC=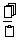 ×
×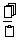 ×4×4=4.
×4×4=4.
即:S四边形CHGK的面积为4,是一个定值,在旋转过程中没有变化.
(2)∵AC=BC=4,BH=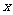 ,∴CH=4-
,∴CH=4-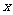 ,CK=
,CK=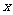 .由S△GHK=S四边形CHGK-S△CHK,
.由S△GHK=S四边形CHGK-S△CHK,
得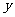 =
= ∴
∴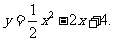 ∵0°<α<90°,∴0<
∵0°<α<90°,∴0<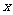 <4.
<4.
(3)存在.
根据题意,得 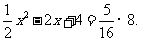
解这个方程,得 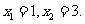
即:当 或
或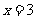 时,△GHK的面积均等于△ABC的面积的
时,△GHK的面积均等于△ABC的面积的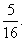
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com