
5.同一平面上的四个点,过每两点画一直线,则直线的条数是( )
A. 1 B. 4 C. 6 D. 1或4或6
4.若⊙O所在平面内一点P到⊙O上的点的最大距离为a,最小距离为b(a>b),则此圆的半径为( )
A. 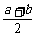 B.
B. 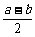 C.
C.
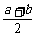 或
或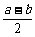 D. a+b或a-b
D. a+b或a-b
3. 已知等腰三角形一腰上的中线将它的周长分为9和12两部分,则腰长为,底边长为_______.
2. 若(x2-x-1)=1,则x=___________.
1.已知AB是圆的直径,AC是弦,AB=2,AC=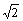 ,弦AD=1,则∠CAD= .
,弦AD=1,则∠CAD= .
80. (2009荆门)如图,在□ABCD中,∠BAD为钝角,且AE⊥BC,AF⊥CD.
(1)求证:A、E、C、F四点共圆;
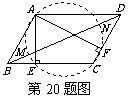 (2)设线段BD与(1)中的圆交于M、N.求证:BM=ND.
(2)设线段BD与(1)中的圆交于M、N.求证:BM=ND.
79. 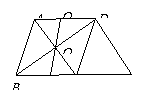 (2009中山)在菱形ABCD中,对角线AC与BD相交于点O,AB=5,AC=6. 过D点作DE//AC交BC的延长线于点E.
(2009中山)在菱形ABCD中,对角线AC与BD相交于点O,AB=5,AC=6. 过D点作DE//AC交BC的延长线于点E.
(1)求△BDE的周长;
(2)点P为线段BC上的点,连接PO并延长交AD于点Q.
求证:BP=DQ.
78. (2009中山)(1)如图1,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G. 求证:阴影部分四边形OFCG的面积是△ABC面积的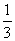 .
.
(2)如图2,若∠DOE保持120º角度不变.
 求证:当∠DOE绕着O点旋转时,由两条半径
求证:当∠DOE绕着O点旋转时,由两条半径
和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC面积的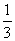 .
.
77. 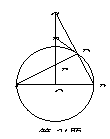 (2009仙桃))如图,AB为⊙O的直径,D是⊙O上的一点,过O点作AB的垂线交AD于点E,交BD的延长线于点C,F为CE上一点,且FD=FE.
(2009仙桃))如图,AB为⊙O的直径,D是⊙O上的一点,过O点作AB的垂线交AD于点E,交BD的延长线于点C,F为CE上一点,且FD=FE.
(1)请探究FD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,BD=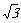 ,求BC的长.
,求BC的长.
76. (2009遂宁)如图,以BC为直径的⊙O交△CFB的边CF于点A,BM平分
∠ABC交AC于点M,AD⊥BC于点D,AD交BM于点N,ME⊥BC于点E,AB2=AF·AC,cos∠ABD=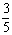 ,AD=12.
,AD=12.
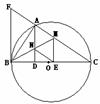 ⑴求证:△ANM≌△ENM;
⑴求证:△ANM≌△ENM;
⑵求证:FB是⊙O的切线;
⑶证明四边形AMEN是菱形,并求该菱形的面积S.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com