2、考点要求

①、掌握列方程和方程组解应用题的方法，能够熟练运用列方程和方程组解应用题。

②、通过列方程和方程组解应用题，提高分析问题和解决问题的能力。

[方法指导]

1、知识网络

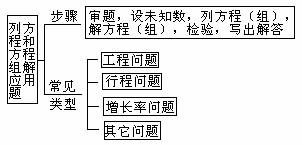
2、考点要求

①、理解一元二次根的判别式，会根据根的判别式判断一元二次方程的根的情况。

②、掌握一元二次方程根与系数的关系，会用它们由已知一元二次方程的一根求另一根与未知数的系数，会求与一元二次方程两个根有关的代数式的值，已知两根会利用根与系数的关系求出方程。

③、会利用一元二次方程根的判别式和根与系数的关系解有关的一元二次方程的综合题。

1、考点要求：

①能够根据具体问题中的数量关系，列出方程，体会方程是刻画现实世界的一个有效的数学模型。 ②经历用观察、画图或计算器等手段估计方程解的过程。 ③会解一元一次方程、简单的二元一次方程组、可化为一元一次方程的分式方程(方程中的分式不超过两个)。 ④理解配方法，会用因式分解法、公式法、配方法解简单的数字系数的一元二次方程。 ⑤能根据具体问题的实际意义，检验结果是否合理。 二、不等式与不等式组 ①能够根据具体问题中的大小关系了解不等式的意义，并探索不等式的基本性质。 ②会解简单的一元一次不等式，并能在数轴上表示出解集。会解由两个一元一次不等式组成的不等式组，并会用数轴确定解集。 ③能够根据具体问题中的数量关系，列出一元一次不等式和一元一次不等式组，解决简单的问题。　　　　　　　　　　

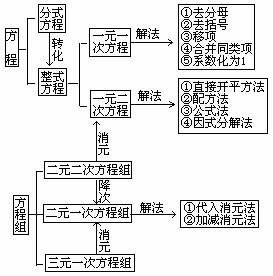
1、知识网络：

10．如图1所示，直角梯形OABC的顶点A、C分别在y轴正半轴与x轴负半轴上．过点B、C作直线l．将直线l平移，平移后的直线l与x轴交于点D与y轴交于点E．

(1)将直线l向右平移，设平移距离CD为t(t≥0)，直角梯形OABC被直线l扫过的面积(图中阴影部份)为S，S关于t的函数图象如图2所示， OM为线段，MN为抛物线的一部分，NQ为射线，N点横坐标为4．

①求梯形上底AB的长及直角梯形OABC的面积；

②当2＜t＜4时，求S关于t的函数解析式；

(2)在第(1)题的条件下，当直线l向左或向右平移时(包括l与直线BC重合)，在直线AB上是否存在点P，使△PDE为等腰直角三角形？若存在，请直接写出所有满足条件的点P的坐标；若不存在，请说明理由．

9．如图，⊙O的半径为1，正方形ABCD顶点B坐标为(5，0)，顶点D在⊙O上运动．

(1)当点D运动到与点A、O在同一条直线上时，试证明直线CD与⊙O相切；

(2)当直线CD与⊙O相切时，求CD所在直线对应的函数关系式；

(3)设点D的横坐标为x，正方形ABCD的面积为S，求S与x之间的函数关系式，并求出S的最大值与最小值．

8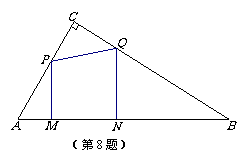．△ABC中，∠C＝90°，∠A＝60°，AC＝2cm．长为1cm的线段MN在△ABC的边AB上沿AB方向以1cm/s的速度向点B运动(运动前点M与点A重合)．过M、N分别作AB的垂线交直角边于P、Q两点，线段MN运动的时间为ts．

(1)若△AMP的面积为y，写出y与t的函数关系式(写出自变量t的取值范围)；

(2)线段MN运动过程中，四边形MNQP有可能成为矩形吗？若有可能，求出此时t的值；若不可能，说明理由；

(3)t为何值时，以C、P、Q为顶点的三角形与△ABC相似？

7．如图，A是半径为12cm的⊙O上的定点，动点P从A出发，以2πcm/s的速度沿圆周逆时针运动，当点P回到A地立即停止运动.

(1)如果∠POA＝90°，求点P运动的时间；

(2)如果点B是OA延长线上的一点，AB＝OA，那么当点P运动的时间为2s时，判断直线BP与⊙O的位置关系，并说明理由．

6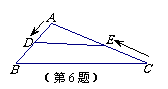．如图，在钝角三角形ABC中，AB＝6cm，AC＝12cm，动点D从A点出发到B点止，动点E从C点出发到A点止．点D运动的速度为1cm/秒，点E运动的速度为2cm/秒．如果两点同时运动，那么当以点A、D、E为顶点的三角形与△ABC相似时，运动的时间是　　　　　　　 (　 　)

A．3秒或4.8秒　　 B．3秒　　　 C．4.5秒　　　 D．4.5秒或4.8秒