
6.设a、b、c为实数,下列结论不正确的是( )
A.若a>b,c=d,则a-c>b-d.
B.若a>b,则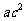 >
>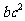 .
C.若
.
C.若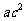 >
>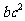 ,则a>b.
D.若
,则a>b.
D.若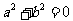 ,则 a=b=0.
,则 a=b=0.
5、二元一次方程组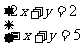 的解是( )
的解是( )
A、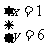 B、
B、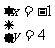 C、
C、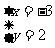 D、
D、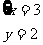
4、设 的两根,那么
的两根,那么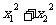 的值为( )
的值为( )
A、3 B、-3 C、6 D、-6
3、如果关于x的一元二此方程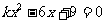 有两个不相等的实数根,那么k的取值范围是( )
有两个不相等的实数根,那么k的取值范围是( )
A、k<1 B、k≠0 C、 k<1且k≠0 D、k>1
2、下列一元方程中,没有实数根的是( )
A、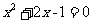 B、
B、
C、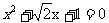 D、
D、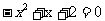
1、方程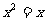 的解是( )
的解是( )
A、1 B、0 C、1或0 D、无解
80.096=80(1+0.000012t)
去括号得:80.096=80+0.00096t
移项、合并同类项得:0.096=80+0.00096t
化系数为1得:t=100
解法二:解关于t的方程:l=l0(1+at)
去括号得:l=l0+a l0t
移项得:a l0t= l-l0
由条件知a≠0,l0≠0,∴a l0≠0,∴t=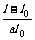
当l=80.096,l0=80,a=0.000012时
t=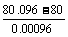 =100
=100
例3、的解法二,是利用解方程的方法对公式变形,方法是:将所求字母t当作未知数,其余字母当作已知数,解字母方程,得到用含有作已知数的字母的代数式表示所求字母t,最后求t的值变为求代数式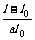 的值。
的值。
例4、当k取何值时,关于x的方程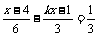 ⑴有解?⑵解为正整数。
⑴有解?⑵解为正整数。
解:解关于x的方程: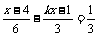
去分母得:x-4-2kx+2=2
移项、合并同类项得:(1-2k)x=4
只有当1-2k≠0时,即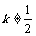 时,方程有唯一解是
时,方程有唯一解是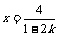
要使方程的解为正整数,必须1-2k=1或1-2k=2或1-2k=4
解得k=0或k=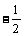 或
或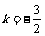 时,方程有正整数解为:
时,方程有正整数解为:
x=4或x=2或x=1
例5、若关于x的方程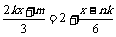 无论k为何值时,它的解总是x=1,求m、n的值。
无论k为何值时,它的解总是x=1,求m、n的值。
解:∵k可为任何值,∴让k分别取0和1
∴当k=0,x=1时,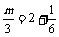 ,得m=
,得m=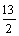
当k=1,x=1时,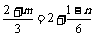 ,∵m=
,∵m=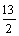 已求得
已求得
∴ ,∴n=-4
,∴n=-4
所以m、n的值分别是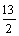 、-4
、-4
例6、解方程: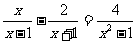
解:原方程变形为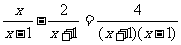
方程两边都乘以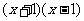 ,去分母并整理得
,去分母并整理得 ,
,
解这个方程得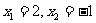 。
。
经检验,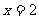 是原方程的根,
是原方程的根,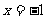 是原方程的增根。
是原方程的增根。
∴原方程的根是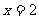 。
。
说明:去分母将分式方程转化为整式方程是解分式方程的基本方法,验根只需将结果代入最简公分母即可。
例7.解下列方程
(1)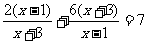
(2)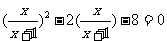
分析:(1)、(2)都是分式方程,可以通过去分母直接求;但通过观察发现(1)中两个分式互为倒数;(2)可以看成是关于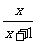 的二次方程。所以(1)和(2)都可以用换元法求解。
的二次方程。所以(1)和(2)都可以用换元法求解。
解(1)设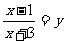 ,那么
,那么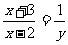 ,原方程变形为
,原方程变形为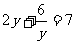 ,
,
整理得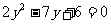 ,解这个方程得
,解这个方程得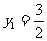 ,
,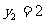 。
。
当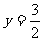 时,即
时,即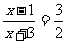 ,去分母得
,去分母得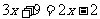 ,解得
,解得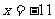 。
。
当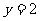 时,即
时,即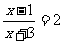 ,去分母得
,去分母得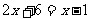 ,解得
,解得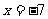 。
。
检验:把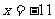 ,
,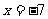 分别代入原方程的分母,各分母都不等于0,所以它们都是原方程的根。
分别代入原方程的分母,各分母都不等于0,所以它们都是原方程的根。
(2)设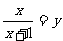 ,则原方程变形为
,则原方程变形为 ,
,
解这个方程得,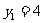 ,
,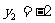 。
。
当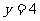 时,
时,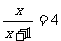 ,解得
,解得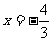 ;
;
当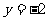 时,
时,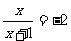 ,解得
,解得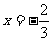 。
。
经检验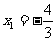 ,
,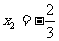 都是原方程的根。
都是原方程的根。
说明:换元法是解分式方程常用的方法,使用此法要善于发现方程的特征,寻找系数之间的关系,使用换元法解题求得结果后仍需要验根。
例8、解方程组
(1)、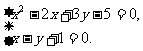
(2)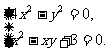
分析:(1)是由一个二元二次方程和二元一次方程组成的方程组,可以由②得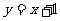 ,并代入①消元即可。
,并代入①消元即可。
(2)是有两个二元二次方程组成的方程组,而由①可以得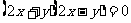 ,这就把原方程组变为
,这就把原方程组变为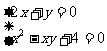
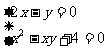 这两个方程组都是(1)的形式,与(1)方法相同,代入消元即可。
这两个方程组都是(1)的形式,与(1)方法相同,代入消元即可。
解:(1)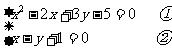
由②得 ,把③代入①得
,把③代入①得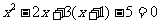 ,
,
整理得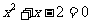 。解得
。解得 ,
, 。
。
将 ,
, 分别代入③得
分别代入③得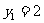 ,
,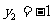
∴原方程组的解为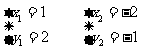
(2)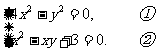
由①得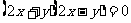 ,∴
,∴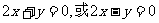 。
。
它们与方程②分别组成两个方程组:
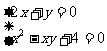
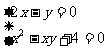
解方程组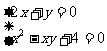 可知,此方程组无解;
可知,此方程组无解;
解方程组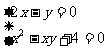 得
得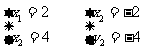
所以原方程组的解是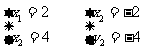
说明:解方程组的基本思路就是消元和降次,要根据方程组的特点选取适当方法。
例9、关于x的方程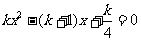 有两个不相等的实数根.
有两个不相等的实数根.
(1)、求k的取值范围;
(2)、是否存在实数k ,使方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由。
解:(1)由题意可知,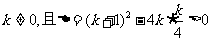
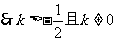 。
。
(2)不存在。
设方程的两根是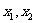 。
。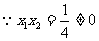 ,
,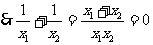 。
。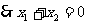 。
。
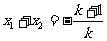 ,
,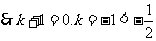 。∴满足条件的实数k不存在。
。∴满足条件的实数k不存在。
说明:(1)判断一元二次方程根的情况,须根据一元二次方程根的判别式,同时要注意对二次项系数不为零的条件不能忽略,(2)与两根有关的代数式,设法转化成有关两根和、两根积的式子即可。
例10、设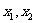 是关于x的方程
是关于x的方程 的两个根,且满足
的两个根,且满足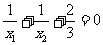 ,求m的值。
,求m的值。
解: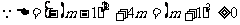 。∴对于任意实数m,方程恒有两个实数根
。∴对于任意实数m,方程恒有两个实数根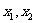 。又
。又 。
。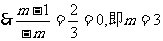 。
。
说明:有关一元二次方程两根和、两根积的计算,需在方程有实数根的前提下方可进行。因此,不能忽略判别式大于等于零的条件。
例11、已知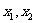 是关于x的一元二次方程
是关于x的一元二次方程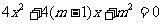 的两个非零实数根,问
的两个非零实数根,问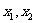 能否同号?若能同号,请求出相应的m的取值范围;若不能同号,请说明理由。
能否同号?若能同号,请求出相应的m的取值范围;若不能同号,请说明理由。
解:∵关于x的一元二次方程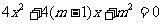 有两个非零实数根,
有两个非零实数根,
则有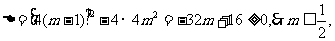
又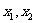 是关于x的一元二次方程
是关于x的一元二次方程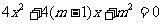 的两个实数根,
的两个实数根,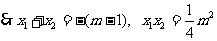 。假设
。假设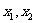 同号,则有两种可能:
同号,则有两种可能:
①若 即
即
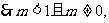
此时m的取值范围是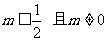 。
。
②若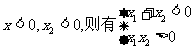 即
即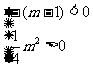
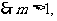
而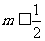 时方程才有实数根,∴此种情况不可能。
时方程才有实数根,∴此种情况不可能。
综上所述,当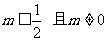 时,方程的两实根同号。
时,方程的两实根同号。
说明:此题为“探索型”试题,这类问题需要在解题过程中探索出结论,这类问题的结论不明确,但与条件有着密切的联系,解题时需灵活思考,探索出条件可能产生的结论。
例12、近几年我省高速公路的建设有了较大的发展,有力地促进了我省的经济建设,正在修建的某段高速公路要招标,现有甲、乙两个工程队,若甲、乙两队合作24天可以完成,需费用120万元,若甲单独做20天后,剩下的工程由乙做,还需40天才能完成,这样需费用110万元。问:(1)甲、乙两队单独完成此项工程,各需要多少天?(2)甲、乙两队单独完成此项工程,各需要费用多少万元?
解:(1)设甲、乙两队单独完成此项工程分别需要x天,y 天。根据题意得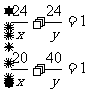
解这个方程组得x=30,y=120 .
经检验x=30,y=120是方程组的解。
(2)设单独完成此项工程,甲需费用m万元,乙需费用n万元,根据题意,得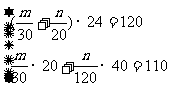
解这个方程组得m=135,n=60 .
答:甲单独完成此项工程需要30天,乙单独完成此项工程需要120天。甲、乙两队单独完成此项工程,分别需要费用135万元、60万元。
说明:此题是工程问题,这类问题涉及到工作时间、工作效率、工作总量之间的关系,基本关系式是 。在问题中,当工作总量不知道时,即只给出单位时间内完成总工作量的几分之几时,通常把总工作量看成“1”。
。在问题中,当工作总量不知道时,即只给出单位时间内完成总工作量的几分之几时,通常把总工作量看成“1”。
例13、某省重视治理水土流失问题,2001年治理了水土流失面积400平方公里,计划今、明两年每年治理水土流失面积都比前一年增长一个相同的百分数,到2003年底使这三年治理的水土流失面积达到1324平方公里,求该省今明两年治理水土流失面积每年增长的百分数。
解:设每年增长的百分数是x,根据题意得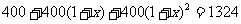
解这个方程得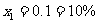 ,
,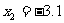 (不合题意舍去)。
(不合题意舍去)。
答:每年增长的百分数是10%。
说明:此题是增长率问题,要理解题意,这里给出的是三年治理水土流失面积的总和,而不是第三年治理的水土流失面积。
例14、某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两道侧门大小也相同。安全检查中,对4道门进行了测试:当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生;当同时开启一道正门和一道侧门时,4分钟内可以通过800名学生。
(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况时因学生拥挤,出门的效率将降低20%。安全检查规定:在紧急情况下全大楼的学生应在5分钟内通过这4道门安全撤离。假设这栋教学大楼每间教室最多有45名学生,问:建造的这4道门是否符合安全规定?请说明理由。
解:(1)设平均每分钟一道正门可以通过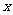 名学生,一道侧门可以通过
名学生,一道侧门可以通过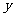 名学生,由题意得:
名学生,由题意得:
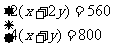
解得: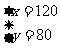
答:平均每分钟一道正门可以通过120名学生,一道侧门可以通过80名学生。
(2)这栋楼最多有学生4×8×45=1440(名)
拥挤时5分钟4道门能通过: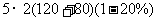 =1600(名)
=1600(名)
∵1600>1440
∴建造的4道门符合安全规定。
说明:运用数学知识解决社会热点问题和实际生活中的问题,是中考命题的一大热点。
解题的关键是理解题意,将实际问题转化为数学问题。
专题练习
3、大家知道,二次函数有顶点式(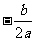 ,
,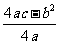 ),这大家要记住,很重要,因为在上面已经说过了,一元二次方程也是二次函数的一部分,所以他也有自己的一个解法,利用他可以求出所有的一元一次方程的解。
4、一元二次方程和二次函数的关系
大家已经学过二次函数(即抛物线)了,对他也有很深的了解,图像解法,在图象中表示等等,其实一元二次方程也可以用二次函数来表示,其实一元二次方程也是二次函数的一个特殊情况,就是当y=0的时候就构成了一元二次方程了。那如果在平面直角坐标系中表示出来,一元二次方程就是二次函数中,图象与X轴的交点。也就是该方程的解了。
[例题选讲]
),这大家要记住,很重要,因为在上面已经说过了,一元二次方程也是二次函数的一部分,所以他也有自己的一个解法,利用他可以求出所有的一元一次方程的解。
4、一元二次方程和二次函数的关系
大家已经学过二次函数(即抛物线)了,对他也有很深的了解,图像解法,在图象中表示等等,其实一元二次方程也可以用二次函数来表示,其实一元二次方程也是二次函数的一个特殊情况,就是当y=0的时候就构成了一元二次方程了。那如果在平面直角坐标系中表示出来,一元二次方程就是二次函数中,图象与X轴的交点。也就是该方程的解了。
[例题选讲]
例1、解方程:⑴0.5x-0.7=6.5-1.3x
⑵3.5x+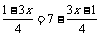
⑶17{6[5(3x-12)+10]+31}-2=15
⑷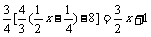
⑸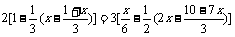
解:⑴原方程化为:5x-7=65-13x……(利用等式性质2,两边都乘以10)
移项、合并同类项得:18x=72,∴x=4
⑵原方程化为3.5x+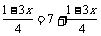 ……(
……(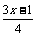 与
与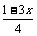 是互为相反数)
是互为相反数)
移项得:3.5x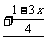
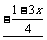 =7
=7
合并同类项得:3.5x=7,∴x=2
⑶移项、合并得:17{6[5(3x-12)+10]+31}=17
两边除以17,并移项得:6[5(3x-12)+10]=-30
两边除以6,并移项得:5(3x-12)=-15
两边除以5: 3x-12=-3
移项、合并同类项得: 3x=9,x=3
⑷去括号得: 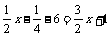
移项、合并同类项得: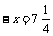 ∴
∴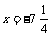
⑸去括号得: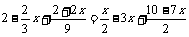
通分化简: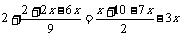
即 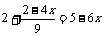
去分母得:18+2-4x=45-54x
移项、合并同类项得:50x=25,∴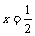
例2、解关于x的方程⑴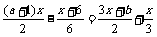 (a≠3);⑵(m+1)x=n-x
(a≠3);⑵(m+1)x=n-x
解:⑴去分母得:3(a+1)x-(x+6)=3(3x+b)+2x
去括号得:3ax+3x-x-6=9x+3b+2x
移项、合并同类项得:(3a-9)x=3b+6,即(a-3)x=b+2
∵a≠3,∴a-3≠0,∴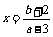
⑵去括号得:mx+x=n-x
移项、合并同类项得:(m+2)x=n
①当m≠-2时,原方程有唯一解:x=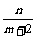
②当m=-2、n=0时,原方程有无数个解
③当m=-2、n≠0时,原方程无解
例3、在公式l=l0(1+at)中,已知l=80.096,l0=80,a=0.000012,求t。
解法一:把l=80.096,l0=80,a=0.000012代入公式中,得
2、解一元二次方程和一元二次方程的运用在中考内十分活跃,几乎每次中考都一定会有这样的题目,所以我在这里说一下。在解方程的时候,因为未知数的项的次数为2,所以解相应的也有2个(未知数的次数决定方程的解),注意的一点是,在计算题的时候,要灵活应用公式法,配方法,分解因式法,在解x=x2时,注意不要失根。
1.方程和方程组是解决应用题、实际问题和许多方面的数学问题的重要基础知识,应用范围非常广泛。很多数学问题,特别是有未知数的几何问题,就需要用方程或方程组的知识来解决,在解决问题时,把某个未知量设为未知数,根据有关的性质、定理或公式,建立起未知数和已知数间的等量关系,列出方程或方程组来解决,这就是方程思想。具有方程思想就能够很好地求得问题中的未知元素或未知量,这对解决和计算有关的数学问题,特别是综合题,是非常需要的。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com