
1.解应用题的一般步骤:
(1)审题,找等量关系式.
(2)设未知数,列方程(组).
(3)解方程(组).
(4)检验,作答.
3.二元二次方程组.
解法:消元、转化为一元二次方程或降次转化为二元一次方程组.
返回
2.三元一次方程组:
(1)一般形式
(2)解法:代人法和加减法.
1.二元一次方程组:
(1)一般形式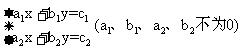
(2)解法:代人法和加减法.
(3)解的个数:惟一解,无数个解,无解三种情况.
3.分式方程根的检验:分式方程必须验根,一般是把求得的未知数的值代人最简公分母,使得公分母不为。的根就是原方程的根,使得公分母为。的根就是原方程的增根,应舍去.
返回
2.分式方程的解法:①去分母法,②换元法.
1.分母中含有未知数的方程叫分式方程.
5.一元二次方程根与系数的关系(韦达定理):
①若一元二次方程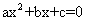 的两根是
的两根是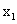 、
、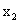 ,则
,则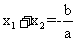 ,
,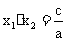 ,特别地,当
,特别地,当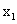 、
、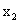 是
是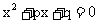 的两根,则有
的两根,则有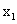 +
+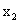 =-p,
=-p,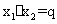 .
.
②以两个数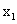 、
、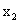 为根的一元二次方程是:
为根的一元二次方程是: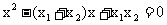
说明:根与系数的关系定理最常见的用法有:(1)由一根求另一根及字母系数的取值范围;(2)求与两根有关代数式的值;(3)构造新方程;(4)解决存在性问题。
另外,上述定理中系数都是一元二次方程一般形式下的,不能搞错。应用根的判别式时,要注意a≠0 这一条件。应用根与系数的关系定理时,也要注意△≥0这一隐含条件,它们经常是容易忽视的条件,也是中考考试题常考的重点内容。
返回
4.一元二次方程根的判别式: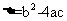
当△>0时,方程有两个不相等的实数根.
当△=0时,方程有两个相等的实数根.
当△<0时,方程没有实数根.
说明:根的判别式最常见的用法用:(1)不解方程判别一元二次方程根的情况;(2)由方程根的情况确定某些字母的值或范围;(3)进行有关的证明。
3.一元二次方程的解法:直接开平方法,配方法,公式法,因式分解法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com