
3.已知正数a和b,有下列命题:
(1)若a+b=2,则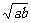 ≤1;(2)若a+b=3,则
≤1;(2)若a+b=3,则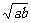 ≤
≤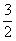 ;(3)若a+b=6,则
;(3)若a+b=6,则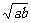 ≤3.
≤3.
根据以上三个命题所提供的规律猜想:若a+b=9,则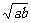 ≤______.并就此规律写出其一般表达式______.
≤______.并就此规律写出其一般表达式______.
2.观察下列各式;(x-1)(x+1)=x2-1,(x-1)(x2+x+1)=x3-1,(x-1)(x3+x2+x+1)=x4-1,根据前面各式的规律可得(x-1)(xn+xn-1+…+x+1)=______.(其中n为正整数)
1.观察下列各式:
2×4=32-1;3×5=42-1;4×6=52-1,…,10×12=112-1,…将你猜想的规律用只含一个字母的式子表示出来______.
5.能根据具体问题的实际意义,检验结果是否合理。
返回
课程标准和原教学大纲之间的区别:
|
知识板块 |
删去的内容 |
|
方程与方程组 |
删去了“三元一次方程组及解法举例”、解一元二次方程的“直接开方法”、一元二次方程的根的“判别式”、二次三项式的“因式分解”、“可化为一元二次方程的分式方程”、“增根与验根”、“换元法”、“二元二次方程”、“二元二次方程组”、“由一个二元一次方程和一个二元二次方程组成的方程组的解法”等内容。 |
返回
复习指导:
复习好这部分知识要做到:弄清概念;灵活掌握解法;注意“配方法”、“换元法”等数学方法和“转化”的数学思想的应用;具有“学数学、用数学”的意识和提高分析问题的能力。并且注意观察实际生活,关心国民经济,努力学好数学基础知识,熟练掌握并正确应用到解题中去。
(1)掌握一元一次方程的标准形式ax+b=0(a≠0)和一元二次方程的一般形式 ax2+bx+c=0(a≠0),重视其中a≠0的条件。如方程(m-1)2+3mx-7=0只有在m≠1时才能称为一元二次方程。
(2)对一元二次方程和二元一次方程组进行变形的依据是方程的基本性质:①方程两边都加上或减去同一个整式,方程的解不变;②方程两边都乘或除以同一不为0的数,方程的解不变。
(3)熟练应用“代入消元法”和“加减消元法”解二元一次方程组,对简单的二元二次方程组要求会用“代入法”、“加减法”、和因式分解的方法进行消元或降次。
(4)列方程或方程组解应用问题是中学阶段的又一重要内容,它的实质是把生活和生产中的实际问题转化为数学问题,再把数学问题通过数学符号转化为方程问题,其中分析等量关系和列出方程是解题中的关键步骤。对于同一个问题,由于思路不同可能会列出不同的方程,而同一个方程对应的可能是不同内容的实际问题。因此,不能企图用一个公式、一个法则和分几个类型就能解决好实际应用问题,重要的学会分析问题(具体问题具体分析)。平时练习时对以下几点常见错误给予重视:
①对方程中已知量与未知量之间的基本关系不清楚,产生列方程的错误。
②在解方程中出现计算错误。
③忘记检验和答题。
(5)一元二次方程根的判别式和根与系数的关系是传统中考热点,但不在课标要求的范围之内,复习时不要设计这些内容。
返回
4.理解配方法,会用因式分解、公式法、配方法解简单的数字系数的一元二次方程。
3.会解一元一次方程、简单的二元一次方程组、可化为一元一次方程的分式方程(方程中的分式不超过两个)。
2.经历用观察、画图或计算器等手段估计方程解的过程。
1.能够根据具体问题中的数量关系,列出方程,体会方程是刻画显示世界的一个有效的数学模型。
3.解应用题常用方法:
①直译法:即将题目中关键性语句或数量关系式写成代数式或等式,然后列方程(组)解答.
②线示法:即用线段关系来表示题中数量关系.
③图示法:即利用图表来表示题中的数量关系,使数量关系式更为直观,便于更好地理解.
返回
2.应用题常见类型及等量关系式:
①工程问题:工作效率(和)×工作时间=工作量.
工程问题常把工作总量看做单位“1”.
②行程问题;路程=速度(和)×时间.
常见问题:相遇问题,追及问题.
③水(空)航行问题:
顺流速度=静水(风)速度十水流(风)速度.
逆流速度=静水(风)速度一水流(风)速度.
④增长率问题:增长后的量=增长前的量×(1+增长率)
⑤浓度(溶液配制)问题: .
.
溶液质量=溶质质量+溶剂质量.
常见问题:溶液的稀释或浓缩,溶液的混合与配制.
⑥数字问题
多位数 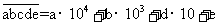 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com