
22.(2006广东深圳中考,22)如图1-3-9,在平面直角坐标系xOy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C、D两点,且C为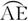 的中点,AE交y轴于G点,若点A的坐标为(-2,0),AE=8.
的中点,AE交y轴于G点,若点A的坐标为(-2,0),AE=8.

图1-3-9
(1)求点C的坐标.
(2)连结MG、BC,求证:MG∥BC.
(3)如图1-3-10,过点D作⊙M的切线,交x轴于点P.动点F在⊙M的圆周上运动时,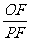 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律.
的比值是否发生变化,若不变,求出比值;若变化,说明变化规律.

图1-3-10
答案:(1)解:方法一:∵直径AB⊥CD,∴CO= CD.
CD.
∵ ,C为
,C为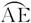 的中点,
的中点,
∴ .∴
.∴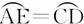 .
.
∴CD=AE.∴CO= CD=4.
CD=4.
∴C点的坐标为(0,4).
方法二:连结CM,交AE于点N,
∵C为 的中点,M为圆心,
的中点,M为圆心,
∴AN= AE=4,CM⊥AE.
AE=4,CM⊥AE.
∴∠ANM=∠COM=90°.
在△ANM和△COM中,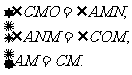
∴△ANM≌△COM.∴CO=AN=4.
∴C点的坐标为(0,4).
(2)证明:设半径AM=CM=r,则OM=r-2.
由OC2+OM2=MC2得42+(r-2)2=r2.
解得r=5.
∵∠AOC=∠ANM=90°,∠EAM=∠MAE,
∴△AOG∽△ANM.∴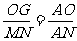 .
.
∵MN=OM=3,即 .∴OG=
.∴OG= .
.
∵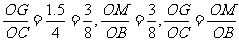 .
.
∵∠BOC=∠BOC,∴△GOM∽△COB.
∴∠GMO=∠CBO.∴MG∥BC.
(说明:直接用平行线分线段成比例定理的逆定理不扣分)
(3)解:连结DM,则DM⊥PD,DO⊥PM,
∴△MOD∽△MDP,△MOD∽△DOP.
∴DM2=MO·MP,
DO2=OM·OP,(说明:直接使用射影定理不扣分)
即42=3·OP.∴OP=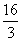 .
.
当点F与点A重合时, ,
,
当点F与点B重合时,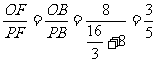 .
.
当点F不与点A、B重合时,连结OF、PF、MF.
∵DM2=MO·MP,∴FM2=MO·MP.
∴ .
.
∵∠AMF=∠FMA,∴△MFO∽△MPF.
∴ .
.
∴综上所述,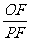 的比值不变,比值为
的比值不变,比值为 .
.
21.(2006云南课改中考,25)如图1-3-8,在直角坐标系中,O为坐标原点,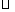 OABC的边OA在x轴上,∠B=60°,OA=6,OC=4,D是BC的中点,延长AD交OC的延长线于点E.
OABC的边OA在x轴上,∠B=60°,OA=6,OC=4,D是BC的中点,延长AD交OC的延长线于点E.

图1-3-8
(1)画出△ECD关于边CD所在直线为对称轴的对称图形△E1CD,并求出点E1的坐标;
(2)求经过C、E1、B三点的抛物线的函数表达式;
(3)请探求经过C、E1、B三点的抛物线上是否存在点P,使以点P、B、C为顶点的三角形与△ECD相似.若存在这样的点P,请求出点P的坐标;若不存在这样的点P,请说明理由.
解:(1)过点E作EE1⊥CD交BC于F点、交x轴于E1点,则E1点为E点的对称点.
连结DE1、CE1,则△CE1D为所画的三角形.

∵△CED∽△OEA, ,
,
∴ .
.
∵EF、EE1分别是△CED、△OEA的对应高,
∴ .∴EF=
.∴EF= EE1.
EE1.
∴F是EE1的中点.
∴E点关于CD的对称点是E1点,△CE1D为△CED关于CD的对称图形.
在Rt△EOE1中,OE1=cos60°×EO= ×8=4.
×8=4.
∴E1点的坐标为(4,0).
(2)∵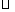 OABC的高为h=sin60°×4=
OABC的高为h=sin60°×4=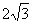 .
.
过C作CG⊥OA于G,则OG=2.
∴C、B点的坐标分别为(2,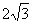 )、(8,
)、(8,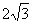 ).
).
∵抛物线过C、B两点,且CB∥x轴,C、B两点关于抛物线的对称轴对称,
∴抛物线的对称轴方程为x=5.
又∵抛物线过E1(4,0),
则抛物线与x轴的另一个交点为A(6,0).
∴可设抛物线为y=a(x-4)(x-6).
∵点C(2,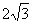 )在抛物线上,
)在抛物线上,
∴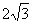 =a(2-4)(2-6),解得a=
=a(2-4)(2-6),解得a=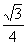 .
.
∴y=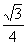 (x-4)(x-6)=
(x-4)(x-6)= .
.
(3)根据两个三角形相似的条件,由于在△ECD中∠ECD=60°,若△BCP与△ECD相似,则△BCP中必有一个角为60°.下面进行分类讨论:
①当P点在直线CB的上方时,由于△PCB中,∠CBP>90°或∠BCP>90°.
∴△PCB为钝角三角形.
又∵△ECD为锐角三角形,
∴△ECD与△CPB不相似.
从而知在直线CB上方的抛物线上不存在点P使△CPB与△ECD相似.
②当P点在直线CB上时,点P与C点或B点重合, 不能构成三角形.
∴在直线CB上不存在满足条件的P点.
③当P点在直线CB的下方时,
若∠BCP=60°,则P点与E1点重合.
此时,∠ECD=∠BCE1,而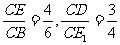 ,
,
∴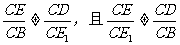 .
.
∴△BCE1与△ECD不相似.
若∠CBP=60°,则P点与A点重合.
根据抛物线的对称性,同理可证△BCA与△CED不相似.
20.我市英山县某茶厂种植 “春蕊牌”绿茶,由历年来市场销售行情知道,从每年的3月25日起的180天内,绿茶市场销售单价y(元)与上市时间t(天)的关系可以近似地用如图1-3-6中的一条折线表示.绿茶的种植除了与气候、种植技术有关外,其种植的成本单价z(元)与上市时间t(天)的关系可以近似地用如图1-3-7的抛物线表示.http://www.1230.org

图1-3-6
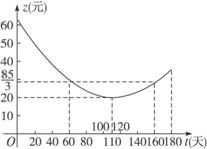
图1-3-7
(1)直接写出图1-3-6中表示的市场销售单价y(元)与上市时间t(天)(t>0)的函数关系式;
(2)求出图1-3-7中表示的种植成本单价z(元)与上市时间t(天)(t>0)的函数关系式;
(3)认定市场销售单价减去种植成本单价为纯收益单价,问何时上市的绿茶纯收益单价最大?
(说明:市场销售单价和种植成本单价的单位:元/500克)
解:(1)依题意,可建立的函数关系式为
y=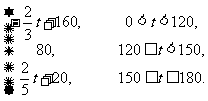
(2)由题目已知条件可设z=a(t-110)2+20.
∵图象过点(60,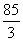 ),
),
∴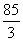 =a(60-110)2+20.∴a=
=a(60-110)2+20.∴a= .
.
∴z= (t-110)2+20(t>0).
(t-110)2+20(t>0).
(3)设纯收益单价为W元,则W=销售单价-成本单价.
故W=
化简得W=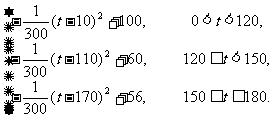
①当W=- (t-10)2+100(0<t<120)时,有t=10时,W最大,最大值为100;
(t-10)2+100(0<t<120)时,有t=10时,W最大,最大值为100;
②当W=- (t-110)2+60(120≤t<150)时,由图象知有t=120时,W最大,最大值为
(t-110)2+60(120≤t<150)时,由图象知有t=120时,W最大,最大值为 ;
;
③当W=- (t-170)2+56(150≤t≤180)时,有t=170时,W最大,最大值为56.
(t-170)2+56(150≤t≤180)时,有t=170时,W最大,最大值为56.
综上所述,在t=10时,纯收益单价有最大值,最大值为100元.
19.(2006上海中考,25)已知点P在线段AB上,点O在线段AB延长线上.以点O为圆心,OP为半径作圆,点C是圆O上的一点.

图1-3-5
(1)如图1-3-5,如果AP=2PB,PB=BO.
求证:△CAO∽△BCO;
(2)如果AP=m(m是常数,且m>1),BP=1,OP是OA、OB的比例中项.当点C在圆O上运动时,求AC∶BC的值(结果用含m的式子表示);
(3)在(2)的条件下,讨论以BC为半径的圆B和以CA为半径的圆C的位置关系,并写出相应m的取值范围.
(1)证明:∵AP=2PB=PB+BO=PO,
∴AO=2PO.∴ .
.
∵PO=CO,∴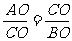 .
.
∵∠COA=∠BOC,∴△CAO∽△BCO.
(2)解:设OP=x,则OB=x-1,OA=x+m,
∵OP是OA、OB的比例中项,
∴x2=(x-1)(x+m),
得x=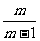 ,即OP=
,即OP=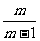 .∴OB=
.∴OB= .
.
∵OP是OA、OB的比例中项,即 .
.
∵OP=OC,∴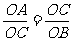 .
.
设圆O与线段AB的延长线相交于点Q,当点C与点P、点Q不重合时,
∵∠AOC=∠COB,∴△CAO∽△BCO.
∴ ;
;
当点C与点P或点Q重合时,可得 =m,
=m,
∴当点C在圆O上运动时,AC∶BC=m.
(3)解:由(2)得,AC>BC,且AC-BC=(m-1)BC(m>1),
AC+BC=(m+1)BC,圆B和圆C的圆心距d=BC,
显然BC<(m+1)BC,∴圆B和圆C的位置关系只可能相交、内切或内含.
当圆B与圆C相交时,(m-1)BC<BC<(m+1)BC,得0<m<2.
∵m>1,∴1<m<2.
当圆B与圆C内切时,(m-1)BC=BC,得m=2.
当圆B与圆C内含时,BC<(m-1)BC,得m>2.
18.(2006广东深圳中考,21)如图1-3-4,抛物线y=ax2-8ax+12a(a<0)与x轴交于A、B两点(点A在点B的左侧),抛物线上另有一点C在第一象限,满足∠ACB为直角,且恰使△OCA∽△OBC.

图1-3-4
(1)求线段OC的长.
(2)求该抛物线的函数关系式.
(3)在x轴上是否存在点P,使△BCP为等腰三角形?若存在,求出所有符合条件的P点的坐标;若不存在,请说明理由.
解:(1)由ax2-8ax+12a=0(a<0)得x1=2,x2=6,
即OA=2,OB=6.
∵△OCA∽△OBC,
∴OC2=OA·OB=2×6.
∴OC=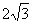 (-
(-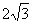 舍去).
舍去).
∴线段OC的长为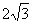 .
.
(2)∵△OCA∽△OBC,
∴ .
.

设AC=k,则BC=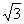 k.
k.
由AC2+BC2=AB2得k2+(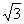 k)2=(6-2)2.
k)2=(6-2)2.
解得k=2(-2舍去).
∴AC=2,BC=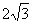 =OC.
=OC.
过点C作CD⊥AB于点D,∴OD= OB=3.
OB=3.
∴CD=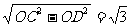 .
.
∴C的坐标为(3,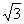 ).
).
将C点的坐标代入抛物线的解析式得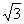 =a(3-2)(3-6),∴a=-
=a(3-2)(3-6),∴a=-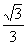 .
.
∴抛物线的函数关系式为y= .
.
(3)①当P1与O重合时,△BCP1为等腰三角形.
∴P1的坐标为(0,0).
②当P2B=BC时,(P2在B点的左侧),△BCP2为等腰三角形.
∴P2的坐标为(6-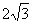 ,0).
,0).
③当P3为AB的中点时,P3B=P3C,△BCP3为等腰三角形.
∴P3的坐标为(4,0).
④当BP4=BC时(P4在B点的右侧),△BCP4为等腰三角形.
∴P4的坐标为(6+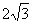 ,0).
,0).
∴在x轴上存在点P,使△BCP为等腰三角形,符合条件的点P的坐标为(0,0),(6-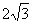 ,0)(4,0),(6+
,0)(4,0),(6+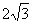 ,0).
,0).
16.在Rt△ABC中,AB=6,BC=8,则这个三角形的外接圆直径是( )
A.5 B.10 C.5或4 D.10或8
解析:BC=8有可能是直角边,也有可能是斜边.
答案:D
15.若解方程 产生增根,则m的值是( )
产生增根,则m的值是( )
A.-1或-2 B.-1或2 C.1或2 D.1或-2
解析:原式化为x2-2x-m-2=0.
原方程有增根,即x=0或x=-1.
答案:D
14.在直角坐标系中,已知点A(-2,0)、B(0,4)、C(0,3),过点C作直线交x轴于点D,使得以D、O、C为顶点的三角形与△AOB相似,这样的直线最多可以作( )
A.2条 B.3条 C.4条 D.6条
答案:C
13.若实数a、b满足a2-8a+5=0,b2-8b+5=0,则 的值为( )
的值为( )
A.-20 B.2 C.2或-20 D.2或20
解析:分a=b,a≠b两种情况.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com