
6.乘积为 1的两个有理数互为倒数.
5.数轴上两个点表示的数,右边的总比左边的大;正数大于0,负数小于0,正数大于负数;两个负数比较大小,绝对值大的反而小.
4.在数轴上,一个数所对应的点与原点的距离叫做该数的绝对值.
正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.
3.如果两个数只有符号不同,那么我们称其中一个数为另一个数的相反数,也称这两个数 互为相反数.0的相反数是0.
2.规定了原点、正方向和单位长度的直线叫做数轴.
1.整数与分数统称为有理数.有理数
2.借助数轴理解相反数和绝对值的意义,会求有理数的相反数与绝对值
1.理解有理数及其运算的意义,并能用数轴上的点表示有理数,会比较有理数的大小.
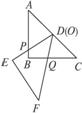
24.(2006湖南常德中考,26)把两块全等的直角三角板ABC和DEF叠放在一起,使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合,其中∠ABC=∠DEF=90°,∠C=∠F=45°,AB=DE=4,把三角板ABC固定不动,让三角板DEF绕点O旋转,设射线DE与射线AB相交于点P,射线DF与线段BC相交于点Q.
(1)如图1-3-12(1),当射线DF经过点B,即点Q与点B重合时,易证△APD∽△CDQ.此时AP·CQ=_________________.
(2)将三角板DEF由图1-3-12(1)所示的位置绕点O沿逆时针方向旋转,设旋转角为α.其中0°<α<90°,问AP·CQ的值是否改变?说明你的理由.
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式.(图1-3-12中(2)(3)供解题用).

图1-3-12
分析:(1)问比较简单但很重要;
(2)类似上问的方法思想.
解:(1)8
(2)AP·CQ的值不会改变,
理由如下: 如右图,在△APD与△CDQ中,∠A=∠C=45°,
∠APD=180°-45°-(45°+α)=90°-α,
∠CDQ=90°-α,即∠APD=∠CDQ.
∴△APD∽△CDQ.∴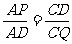 .
.
∴AP·CQ=AD·CD=AD2=( AC)2=8.
AC)2=8.
(3)如图,情形一:当0°<α<45°时,2<CQ<4,即2<x<4,此时两三角板重叠部分为四边形DPBQ,过D作DG⊥AP于G,DN⊥BC于N, ∴DG=DN=2.
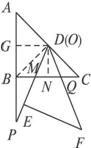
由(2)知AP·CQ=8得AP= .
.
于是y= AB·AC-
AB·AC- CQ·DN-
CQ·DN- AP·DG=8-x-
AP·DG=8-x- (2<x<4).
(2<x<4).
情形二:当45°≤α<90°时,0<CQ≤2时,即0<x≤2,此时两三角板重叠部分为△DMQ,
由于AP= ,PB=
,PB= -4,易证:△PBM∽△DNM,
-4,易证:△PBM∽△DNM,
∴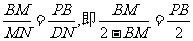 .
.
解得BM=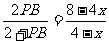 .
.
∴MQ=4-BM-CQ=4-x-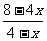 .
.
于是y= MQ·DN=4-x-
MQ·DN=4-x-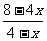 (0<x≤2).
(0<x≤2).
综上所述,当2<x<4时,y=8-x- .
.
当0<x≤2时,y=4-x-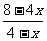 (或y=
(或y=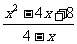 ).
).
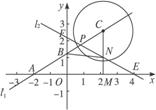
23.(2006浙江中考,24)在平面直角坐标系xOy中,已知直线l1经过点A(-2,0)和点B(0,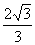 ),直线l2的函数表达式为y=-
),直线l2的函数表达式为y=-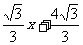 ,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
,l1与l2相交于点P.⊙C是一个动圆,圆心C在直线l1上运动,设圆心C的横坐标是a.过点C作CM⊥x轴,垂足是点M.
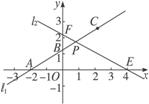
图1-3-11
(1)填空:直线l1的函数表达式是________________,交点P的坐标是________________,∠EPB的度数是________________.
(2)当⊙C和直线l2相切时,请证明点P到直线CM的距离等于⊙C的半径R,并写出R=3 -2时a的值.
-2时a的值.
(3)当⊙C和直线l2不相离时,已知⊙C的半径R=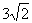 -2,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
-2,记四边形NMOB的面积为S(其中点N是直线CM与l2的交点).S是否存在最大值?若存在,求出这个最大值及此时a的值;若不存在,请说明理由.
解:(1)y=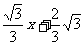 P(1,
P(1,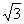 ) 60°
) 60°
(2)设⊙C和直线l2相切时的一种情况如图甲所示,
D是切点,连结CD,则CD⊥PD.
过点P作CM的垂线PG,垂足为G,则Rt△CDP≌Rt△PGC.(∠PCD=∠CPG=30°,CP=PC)
所以PG=CD=R.
当点C在射线PA上,⊙C和直线l2相切时,同理可证.
取R=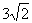 -2时,a=1+R=
-2时,a=1+R=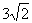 -1或a=-(R-1)=3-
-1或a=-(R-1)=3-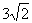 .
.
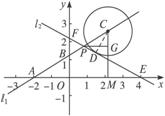
甲
(3)当⊙C和直线l2不相离时,由(2)知分两种情况讨论:①如图乙,当0≤a≤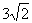 -1时,S=
-1时,S=
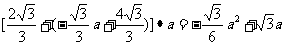 .
.
乙
当a=-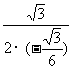 =3时(满足a≤
=3时(满足a≤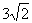 -1),
-1),
S有最大值,此时S最大值=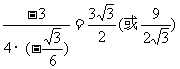 .
.
②当3-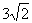 ≤a<0时,显然⊙C和直线l2相切,即a=3-
≤a<0时,显然⊙C和直线l2相切,即a=3-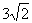 时,S最大,
时,S最大,
此时S最大值= [
[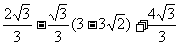 ]·|3-
]·|3-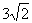 |=
|=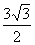 .
.
综合以上①和②,当a=3或a=3-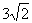 时,存在S的最大值,其最大面积为
时,存在S的最大值,其最大面积为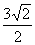 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com