4．经历在具体情境中估计一元二次方程解的过程，发展估算意识和能力．

3．了解一元二次方程及其相关概念，会用配方法、公式法、分解因式法解简单的一元二次方程(数字系数人并在解一元二次方程的过程中体会转化等数学思想．

2．能够利用一元二次方程解决有关实际问题，能根据具体问题的实际意义检验结果的合理性，进一步培养学生分析问题、解决问题的意识和能力．

1．经历由具体问题抽象出一元二次方程的过程，进一步体会方程是刻画现实世界中数量关系的一个有效数学模型．

11、光明中学9年级甲、乙两班在为“希望工程”捐款活动中，两班捐款的总数相同，均多于300元且少于400元．已知甲班有一人捐6元，其余每人都捐9元；乙班有一人捐13元，其余每人都捐8元．求甲、乙两班学生总人数共是多少人？

　 解：设甲班人数为x人，乙班人数为y人，由题意，可得

　 因为x为整数，所以x=34，35，36，37，38，39，40，41，42，43，44．又因为y也是整数，所以x 是8的倍数．所以x=40．则y=44．所以总人数是 84．

　 答：甲、乙两班学生总人数共是84人．

　 点拨：此题中取整数是难点和关键，应根据实际，人数都为整数来确定甲、乙两班的人数.

专题九：一元二次方程

10、一次普法知识竞赛共有30道题，规定答对一道题得4分，答错或不答一道题得－1分，在这次竞赛中，小明获得优秀(90分或 90分以上)则小明至少答对了______道题．

　 解：24 点拨：可设小明至少答对了x道题，则4x+(30－x)×(－1)≥90,　 则x≥24

9、某次“迎奥运”知识竞赛中共20道题，对于每一道题，答对了得10分，答错了或不答扣5分，选手至少要答对(　 )道题，其得分才会不少于95分？

　 A．14　　 B．13　　 C．12　　　 D．11

　 解：B　 点拨：可设至少要答对x道题，得分才不会少于95分，则10x－5(20－x)≥95．解得x≥13．　

8、若不等式组的解集为x＞2，则a的取得范围是( )

　 A. a＜2　　 B. a≤2　　 C. a＞2　　 D. a ≥2

　 解:B 点拨：原不等式组可化为根据“同大取大”的规律，得a＜2已而当a=2时，原不等式组变为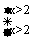’解集也为x＞2．所以正解应为x≤2．选 B．

7、不等式组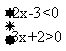’的整数解是______________.

解：0, 1 点拨：要求不等式组的整数解可先求出不等式组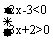的解集为－＜x＜中的整数有0、1，故答案为0、1.　

6、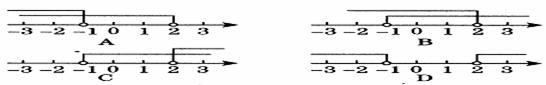不等式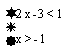’的解集在数轴上可表示为图中的(　 )