5、顶点为(－2，－5)且过点(1，－14)的抛物线的解析式为　　　　　　　　　　　　　　 。

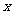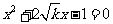4、关于的方程有两个不相等的实数根，则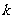的取值范围是　　　　　　　　 。

3、正方形ABCD内接于⊙O，E为DC的中点，如果⊙O的半径为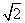,则O点到直线BE的距离为______。

2、一根蜡烛在凸透镜下成一实像，物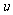距，像距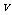和凸透镜的焦距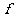满足关系式：

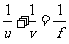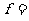。若6cm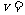，8cm，则物距　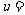　　 厘米。　

1、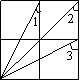如图，已知方格纸中是4个相同的正方形，则∠1+∠2+∠3＝　　　　　 。

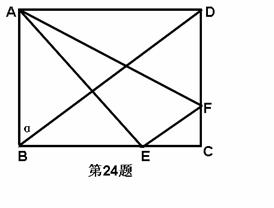
24、(本题14分)如图，在矩形ABCD中，BD=20，AD>AB，设∠ABD=α，已知sinα是方程25x²－35x+12=0的一个实根，点E，F分别是BC，DC上的点，EC+CF=8，设BE=x，

△AEF的面积等于y。

(1)求AB和AD的长；

(2)求出y关于x之间的函数关系式；

(3)当E，F两点在什么位置时，y有最小值？并求出这个最小值。

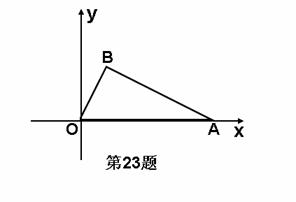
23、(本题12分)如图Rt△ABO的斜边OA在x轴的正半轴上，直角顶点B在第一象限，已知点B(2，4)。

(1)求A点的坐标；

(2)求过O﹑B﹑A三点的抛物线的解析式；

(3)判断该抛物线的顶点P与△ABO的外接圆的位置关系，并说明理由。

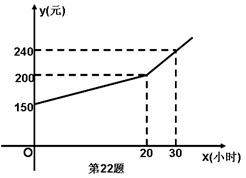
22、(本题12分)为了鼓励小强勤做家务，培养他的劳动意识，小强每月的生活费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的。若设小强每月的家务劳动时间为x小时，该月可得(即下月他可获得)的总费用为y(元)，则y(元)和x(小时)之间的函数图象如图所示。

(1)根据图象，请写出小强每月的基本生活费为多少元？父母是如何奖励小强家务劳动的？

(2)写出当0≤x≤20时，相应的y与x之间的函数关系式；

(3)若小强5月份希望有250元费用，则小强4月份需做家务多少小时？

21、(本题10分)如图，小岛A在港口P的南偏西45⁰，方向，距离港口81海里处，甲船从A出发，沿AP方向以9海里/时的速度驶向港口，乙船从港口P出发，沿南偏东60⁰方向，以18海里/时的速度驶离港口，现两船同时出发。

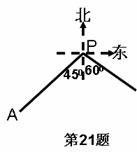(1)出发后几小时两船与港口距离相等？

(2)出发后几小时乙船在甲船的正东方向？(精确到0.1小时)

(参考数据：)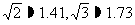

20、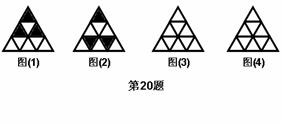(本题8分)图中的大正三角形是由9个小正三角形拼成的，将其部分涂黑，如图(1)，(2)所示。

观察图(1)，图(2)中涂黑部分构成的图案，它们具有如下特征：①都是轴对称图形，②涂黑部分都是三个小正三角形。

请在图(3)，图(4)内分别设计一个新图案，使图案具有上述两个特征。