
5. 如图△ABC中,∠C=90,AB=10cm,AC=8cm,点P从点A开始出发向点C以2cm/s的速度移动,点Q从B点出发向点C以1cm/s的速度移动,若P、Q分别同时从A、B出发,几秒后四边形APQB是△ABC面积的2/3

A. 2 B. 4.5 C. 8 D. 7
答案:A
4. 下列命题中,真命题有( )个。
(1)斜边对应相等的两个直角三角形全等。
(2)顶角对应相等的两个等腰三角形全等。
(3)两腰对应相等的两个等腰三角形全等。
(4)两条直角边对应相等的两个直角三角形全等。
A. 1 B. 2 C. 3 D. 4
答案:A
3. 下面解方程的过程中,正确的是( )
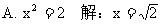
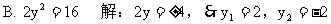
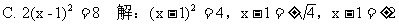
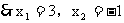
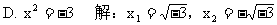
答案:C
2. 顺次连接某四边形各边中点,若得到一个菱形,则这个四边形是( )
A. 正方形 B. 矩形 C. 菱形 D. 以上都不对
答案:B
1. 关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根是0,则a的值为( )
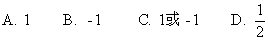
答案:B
23.根据身边生活中的素材,编写两道利用一元二次方程求解的应用题,其中应有一道涉及几何内容的.
实践探索作业评价表
班级 姓名 交卷时间
|
评价人 |
评语 |
成绩 |
|||
|
优 |
良 |
中 |
不理想 |
||
|
学生本人 |
|
|
|
|
|
|
学生家长 |
|
|
|
|
|
|
任课教师 |
|
|
|
|
|
.
九年级上学期期中测试卷
Ⅰ卷 一、1. 4cm;2. 四边形ABCD是菱形;AB = AD,CB = CD;BA = BC,DA = DC;
∠ADB =∠DAC = 90°,…
等;3. 或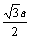 ; 4. ②,③; 5. x1
= -6,x2 = 2; 6. 1,-3; 7. 60°; 8.
; 4. ②,③; 5. x1
= -6,x2 = 2; 6. 1,-3; 7. 60°; 8. 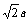 ; 9. 3; 10. . 二、11. C; 12. D; 13. D; 14. B; 15. A; 16. D. 三、17.
; 9. 3; 10. . 二、11. C; 12. D; 13. D; 14. B; 15. A; 16. D. 三、17.
(1)±5;(2) ;(3)
;(3)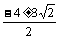 ;(4)
;(4)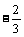 ,
,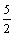 . 18. AD≈227m,BC≈146m; 19. 略; 20. 提示:证ED = AC. 四、21. A类:10cm;B类:5%;C类:(1)20元,(2)15元.
. 18. AD≈227m,BC≈146m; 19. 略; 20. 提示:证ED = AC. 四、21. A类:10cm;B类:5%;C类:(1)20元,(2)15元.
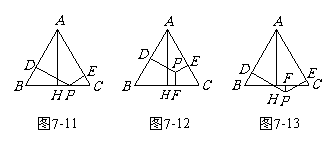
22.已知:等边△ABC和点P,设点P到△ABC三边AB、AC、BC的距离分别为h1、h2、h3, △ABC的高为h.
(1)若点P在BC边上(如图7-11),证明:h1 +h2 +h3 = h;
(2)利用(1)中所提供的信息解决下列问题:
① 当点P在△ABC内部(如图7-12)时,
② 当点P在△ABC外部(如图7-13)时,
结论h1 +h2 +h3 = h是否还成立?若成立,请给出证明;若不成立,h1、h2、h3与h之间又有怎样的关系?请写出你的猜想,并说明理由.
|
纠正错解 |
|
|
|
点 评 |
|
|
小组成员、分工、评价表
Ⅲ卷 实践探索卷
(满分20分,成绩计入总分)
21. (A类6分)如图7-10,从一块长80cm,宽60cm的矩形铁片中间截去一个小矩形,使剩下的长方形框四周的宽度相等,且其面积是原来铁片面积的一半,求这个宽度.
(A类6分)如图7-10,从一块长80cm,宽60cm的矩形铁片中间截去一个小矩形,使剩下的长方形框四周的宽度相等,且其面积是原来铁片面积的一半,求这个宽度.
|
纠正错解 |
|
|
|
点 评 |
|
|
(B类7分)滨江中学某班前年暑假将勤工俭学挣得的班费2000元按一年定期存入银行,去年暑假到期后取出1000元寄往灾区,将剩下的1000元和利息继续按一年定期存入银行,待今年毕业后全部捐给母校. 若今年到期后取得人民币(本息和)1155元,问银行一年定期存款的年利率(假定年利率不变)是多少?
(C类8分)某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元. 为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施. 经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天盈利最多?
Ⅱ卷 合作卷
(答卷可使用计算器,时间30分钟,满分20分,成绩计入总分)
20.已知:如图7-9,Rt△ABC中,∠ACB = 90°,D是斜边AB的中点,AE
= AD,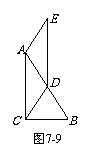 且ED∥AC. 求证:四边形ACDE是平行四边形.
且ED∥AC. 求证:四边形ACDE是平行四边形.
19.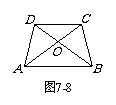 如图7-8,在梯形ABCD中,已知:AB∥DC,对角线AC、BD相交于点O,且OA = OB,求证:梯形ABCD是等腰梯形.
如图7-8,在梯形ABCD中,已知:AB∥DC,对角线AC、BD相交于点O,且OA = OB,求证:梯形ABCD是等腰梯形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com