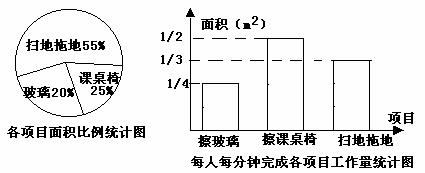
某班13位同学参加每周一次的卫生大扫除，按学校的卫生要求需要完成总面积为80m²的三个项目的任务，三个项目的面积比例和每人每分钟完成各项目的工作量如下图所示：(1)从上述统计图中可知：每人每分钟擦课桌椅　　 m²；擦玻璃、擦课桌椅、扫地拖地的面积分别是　　 m²，　　 m²，　　 m²；(2)如果x人每分钟擦玻璃的面积是ym²，那么y关于x的函数关系式是　　　　　　　 ；(3)他们一起完成扫地和拖地的任务后，把这13人分成两组，一组去擦玻璃，一组去擦课桌椅。如果你是卫生委员，该如何分配这两组的人数，才能最快地完成任务。

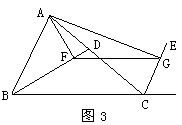
已知：如图1，BD分别是△ABC的外角平分线，过点

A作AF⊥BD，AG⊥CE，垂足分别为F、G，连结FG，延长

AF、AG，与直线BC相交，易证。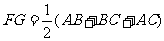

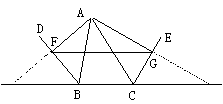若(1)BD、CE分别是△ABC的内角平分线(如图2)；

(2)BD为△ABC的内角平分线，CE为△ABC的外角平分线(如图3)。则在图2、图3两种情况下，线段FG与△ABC三边又有怎样的数量关系？请写出你的猜想，并对其中的一种情况给予证明。

3.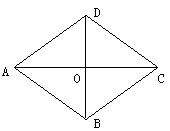如图，菱形ABCD的边长是5，两条对角线交于O点，且AO、BO的长分别是关于x的方程x²+(2m－1)x+m²+3＝0的根，则m的值为(　 )

A．－3 　　 B．5　 　 C．5 或－3　 　 D．－5或3

2.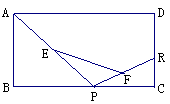矩形ABCD中，R为CD上一定点，P为BC上一动点，

E、F分别是AP、RP的中点，当P从B向C移动时，线段

EF的长度(　 )

A．不变　 　　B．逐渐变大 　　C．逐渐变小 　　D．无法确定

1.若一元二次方程ax²+bx+c＝0中二次项系数、一次项系数和常数项之和为零，那么此方程必有一根为(　　 )

A．0　　　　　　　 B．1　　　　　　　 C．－1　　　　　　 D．±1

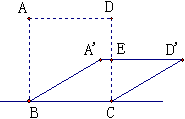
4. 如图，正方形木框ABCD，边长为1，四个角用铰链接着，一边BC固定在桌面上，沿AD方向用力推。正方形变成四边形A′BCD′，设A′D′交DC于点E，当E是DC的中点时，两四边形ABCD、A′BCD′重叠部分的面积是__________。

3.如图，E，F，G，H分别是正方形ABCD各边的

中点，要使中间阴影部分小正方形的面积是5，那么

大正方形的边长应该是　　　　 。

2.已知方程的两根分别是a、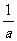，则方程

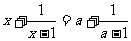的根是　　　　　　 。　

1.请写出一个一元二次方程，使得它的一个根是1，常数项为10：　　　　　　　 。

3.某商场将进货价为30元的台灯以40元售出，平均每月能售出600个。调查表明：这种台灯每上涨1元，其销售量就将减少10个。为了实现平均每月10000元的销售利润，这种台灯的售价应定为多少？这时应进台灯多少个？

请你利用方程解决这一问题。

B　 卷