
4.关于x的方程kx 2 + 3x-1 = 0 有实数根, 则k的取值范围是( )
A. k ≤- B.
k ≥-
B.
k ≥- ,且k ≠0
,且k ≠0
C. k ≥- D.
k > -
D.
k > - 且k≠0
且k≠0
3.如图∠AOP = ∠BOP = 15°PC∥OA , PD⊥OA若PC = 4 ,则PD = ( )
A.1 B. 2 C.4 D.6
2.则△ABC三边距离相等的点是△ABC的( )
A.三条中线的交点 B.三条角平分线交点
C. 三条高的交点 D.三条边的垂直平分线交点
1.如图,AC与BE相互垂直平分,D为垂足,若∠ACB = 56°,则∠E = ( )
A.24° B.34° C.30° D.45°



第1题图 第3题图 第7题图
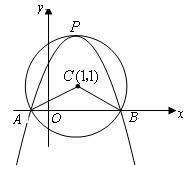
22、(本题9分)如图,在平面直角坐标系中,以点 为圆心,2为半径作圆,交
为圆心,2为半径作圆,交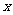 轴于
轴于 两点,开口向下的抛物线经过点
两点,开口向下的抛物线经过点 ,且其顶点
,且其顶点 在⊙C上.
在⊙C上.
(1)求 的大小;
的大小;
(2)写出 两点的坐标;
两点的坐标;
(3)试确定此抛物线的解析式;
(4)在该抛物线上是否存在一点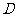 ,使线段
,使线段 与
与 互相平分?若存在,求出点
互相平分?若存在,求出点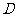 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
21. (本题9分)已知:直线y=-2x+2分别与x轴、y轴相交于点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC,∠BAC=90°,过C作CD⊥x轴于D
(本题9分)已知:直线y=-2x+2分别与x轴、y轴相交于点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC,∠BAC=90°,过C作CD⊥x轴于D
求(1)点A、B的坐标
(2)AD的长
(3)过A、B、C三点的抛物线的解析式
(4)在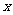 轴上是否存在点
轴上是否存在点 ,使△
,使△ 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.

20、(本题8分).如图1,已知O为坐标原点,点A的坐标为(2,3),⊙A的半径为1,过A作直线l平行于x轴,设l与y轴交点为C,点P在l上运动.
(1)当点P运动到圆上时,求此时点P的坐标
(2)如图2,当点P的坐标为(4,3)时,连结OP,作AM⊥OP于M,
求OP的长和AM的长
(3)在(2)条件下,试判断直线OP与⊙A的位置关系,并说明理由.

图1

图2
19、 (本题8分)某水果批发商销售每箱进价为40元的苹果,市场调查发现,若每箱以50元的价格调查,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(本题8分)某水果批发商销售每箱进价为40元的苹果,市场调查发现,若每箱以50元的价格调查,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
18.(本题7分)如图,某货船以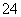 海里/时的速度将一批重要物资从A处运往正东方向的M处,在点
海里/时的速度将一批重要物资从A处运往正东方向的M处,在点 处测得某岛C在北偏东
处测得某岛C在北偏东 的方向上.该货船航行
的方向上.该货船航行 分钟后到达B处,此时再测得该岛在北偏东
分钟后到达B处,此时再测得该岛在北偏东 的方向上,已知在C岛周围
的方向上,已知在C岛周围 海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.
海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由.

17、(本题8分)如图,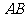 是⊙O的一条弦,
是⊙O的一条弦, ,垂足为
,垂足为 ,交⊙O于点
,交⊙O于点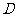 ,
,
 点
点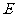 在⊙O上.
在⊙O上.
(1)若 ,求
,求 的度数;
的度数;
(2)若 ,
, ,求
,求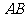 的长.
的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com