
24.作一次社会调查,在较大范围内分组统计每一个人的姓氏,计算出在这一人群中,排在“百家姓”中的前四种姓--“赵、钱、孙、李”分别出现的频率,估计,任找一人,该人姓赵(或姓钱、孙、李)的概率.
实践探索作业评价表
班级 姓名 交卷时间
|
评价人 |
评语 |
成绩 |
|||
|
优 |
良 |
中 |
不理想 |
||
|
学生本人 |
|
|
|
|
|
|
学生家长 |
|
|
|
|
|
|
任课教师 |
|
|
|
|
|
.
九年级上学期期末测试卷
Ⅰ卷 一、1. AB = CD,或AD∥BC,或∠A =∠C,或∠B =∠D等;AB = BC,或BC = CD,或CD = AD,或AD = AB,或AC⊥BD,或AC平分∠BAD,或BD平分∠ABC等; 2. 30m; 3. AC = BC,或CE = CF,或CD⊥AB,或∠A =∠B,或CD平分∠ACB等; 4. 24或8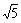 ; 5. 填入任何一组满足m2 =
4n的m、n的值均可,如m =2,n = 1,… 等; 6. y = ; 7. 2; 8. y = ,(-3,-1); 9. ; 10. . 二、11. C; 12. D; 13. B; 14. C; 15. D; 16. A. 三、17. 1小时.
18. 略. 19. y = x +1,y = . 20. (1)从左到右依次是0.9,0.95,0.88,0.91,0.89,0.90;(2)约为0.90. 四、21. 略.
; 5. 填入任何一组满足m2 =
4n的m、n的值均可,如m =2,n = 1,… 等; 6. y = ; 7. 2; 8. y = ,(-3,-1); 9. ; 10. . 二、11. C; 12. D; 13. B; 14. C; 15. D; 16. A. 三、17. 1小时.
18. 略. 19. y = x +1,y = . 20. (1)从左到右依次是0.9,0.95,0.88,0.91,0.89,0.90;(2)约为0.90. 四、21. 略.
Ⅱ卷22.
23.为美化环境,计划在某住宅小区内为一块面积为30平方米,一边长为10米的等腰三角形绿地铺设草皮,请求出这块绿地的另两边长.
小组成员、分工、评价表
|
纠正错解 |
|
|
|
点 评 |
|
|
Ⅲ卷 实践探索卷
(满分20分,成绩计入总分)
22.某汽车公司冲压厂冲压汽车零件的废料都是等腰三角形的小钢板,该冲压厂为了降低汽车零件成本,变废为宝,把这些废料经过切割、焊接,再加工成粉碎机上的两种不同规格的矩形零件,销售给农机厂. 每种矩形的面积正好等于该三角形的面积(每次切割的次数最多两次,切割的损失忽略不计).
(1)请设计两种不同的切割方案,并用简要的文字加以说明;
(2)若要把三角形废料切割、焊接成正方形零件(只切割一次),该三角形废料需满足什么条件?
21.(A类6分)已知:如图8-9,AB = AC,AE = AD.
求证:∠B =∠C.
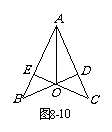 (B类7分)已知:如图8-10,CE⊥AB于点E,BD⊥AC于点D,BD、CE交于点O,且AO平分∠BAC. 求证:OB = OC.
(B类7分)已知:如图8-10,CE⊥AB于点E,BD⊥AC于点D,BD、CE交于点O,且AO平分∠BAC. 求证:OB = OC.
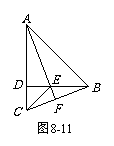 (C类8分)已知:如图8-11,△ABD,△CED都是等腰直角三角形,且D在AC上,AE的延长线与BC交于点F. 请你在图中找出一对全等三角形,并写出证明过程.
(C类8分)已知:如图8-11,△ABD,△CED都是等腰直角三角形,且D在AC上,AE的延长线与BC交于点F. 请你在图中找出一对全等三角形,并写出证明过程.
Ⅱ卷 合作卷
(答卷可使用计算器,时间30分钟,满分20分,成绩计入总分)
20.某射击运动员在同一条件下进行射击训练,成绩如下表所示:
|
射击次数 |
10 |
20 |
50 |
100 |
200 |
500 |
|
射中10环次数 |
9 |
19 |
44 |
91 |
178 |
451 |
|
射中10环频率 |
|
|
|
|
|
|
(1)填写表中射中10环的频率;
(2)估计该运动员射击一次命中10环的概率.
|
纠正错解 |
|
|
|
点 评 |
|
|
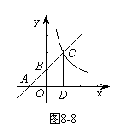
19.如图8-8,已知:一次函数y = kx +b (k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y = (m≠0)的图象在第一象限交于C点,CD垂直于x轴,垂足为D. 若OA = OB = OD = 1,求一次函数和反比例函数的表达式.
18. 画出图8-7所示几何体的三视图.
画出图8-7所示几何体的三视图.
17.人民海关缉私巡逻艇在东海海域执行巡逻任务时,发现在其所处位置O点的正北方向10海里处的A点有一涉嫌走私船只,正以24海里/时的速度向正东方向航行. 为迅速实施检查,巡逻艇立即调整好航向,以24海里/时的速度追赶.在涉嫌船只不改变航向和航速的前提下,巡逻艇需多久才能追上?
16.从不大于20的正整数中任取一个数,则取出的数恰好是3的倍数的概率为( ).
A. B. C. D.
|
纠正错解 |
|
|
|
点 评 |
|
|
15.已知反比例函数y = - 的图象上有两点A (x1,y1),B (x2,y2),且x1<x2,那么,下列结论中正确的是( );
A. y1 < y2 B. y1 = y2 C. y1 > y2 D. y1与 y2的大小不能确定
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com