
2.若代数式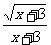 有意义,则
有意义,则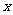 __________.
__________.
1.与点P(3,4)关于中心对称的点的坐标为___________.
27.(6分)依据闯关游戏规则,请你探究“闯关游戏”的奥秘:
(1)用列表的方法表示有可能的闯关情况;
(2)求出闯关成功的概率.

28.(5分)某超市为了促销一批新品牌的商品,设立了一个不透明的纸箱, 纸箱里装有一个红球,2个白球和12个黄球,并规定:顾客每购买50元的新品牌商品, 就能获得一次摸球的机会,如果摸到红球,顾客可以获得一把雨伞,摸到白球,可以获得一个文具盒,摸到黄球,可以获得一支铅笔,甲顾客购此新商品80元,她获得奖品的概率是多少?他得到一把雨伞,一个文具盒,一支铅笔的概率分别是多少?
26.(7分)某商场设了一个可以自由转动的转盘如图,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
(1)计算并完成表格:
|
转动转盘的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
|
落在“钢笔”的次数m |
68 |
111 |
136 |
345 |
564 |
701 |
|
落在“钢笔”的频率 |
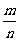 |
|
|
|
|
|
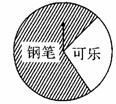 (2)请估计,当n很大时,频率将会接近多少?
(2)请估计,当n很大时,频率将会接近多少?
25.(6分)已知8支球队中有3支弱队,以抽签的方式将这8支球队分为A、B两组,每组4支,求:(1)A、B两组中有一组恰有两支弱队的概率;(2)A组中至少有两支弱队的概率.
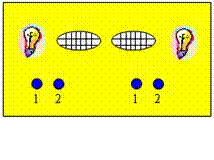
24.(9分)飞镖随机地掷在下面的靶子上.
(1)在每一个靶子中,飞镖投到区域A、B、C的概率是多少?
(2)在靶子1中,飞镖投在区域A或B中的概率是多少?
(3)在靶子2中,飞镖没有投在区域C中的概率是多少?

23.(6分)甲、乙两人各进行一次射击,若两人击中目标的概率均为0.6.求:
(1)两人均击中目标的概率;
(2)至少有1人击中目标的概率.
22.(5分)从数学、语文、英语、 计算机这四门课程中选出两门排在星期一上午第一、二两节课,数学和计算机不能排在一起,语文不能排在第一节, 两节可以排同一门课程,求星期一上午有英语的概率?
21.(5分)口袋里有红、绿、黄三种颜色的球,其中有红球4个,绿球5个,任意摸出1 个绿球的概率是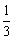 ,求摸出一个黄球的概率?
,求摸出一个黄球的概率?
20.(5分)从男女学生共36人的班级中,选一名班长,任何人都有同样的当选机会,如果选得男生的概率为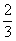 ,求男女生数各多少?
,求男女生数各多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com