
5、 已知⊙O和三点P、Q、R,⊙O的半径为3,OP=2,OQ=3,OR=4,经过这三点中的一点任意作直线总是与⊙O相交,这个点是 ( )
A.P B.Q C.R D.P或Q
4、顺次连结等腰梯形四边中点得到一个四边形,再顺次连结所得四边形四边的中点得到的图形是( )
A、等腰梯形 B、直角梯形 C、菱形 D、矩形
3、.三角形两边的长分别是8和6,第三边的长是一元二次方程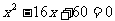 的一个实数根,则该三角形的面积是
( )
的一个实数根,则该三角形的面积是
( )
A、 24 B、 24或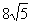 C、
48
D、
C、
48
D、 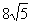
2、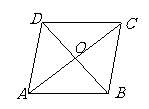 如图,
如图,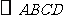 中,对角线
中,对角线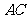 和
和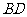 相交于点
相交于点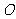 ,如果
,如果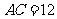 ,
,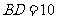 ,
,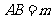 ,那么
,那么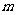 的取值范围是( )
的取值范围是( )
A.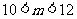 B.
B.
C.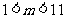 D.
D.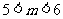
1、在下列式子中,正确的是 ( )
 (A)
(A)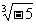 =-
=-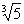 (B)-
(B)-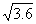 =-0.6(C)√(-13)2 =-13 (D)
=-0.6(C)√(-13)2 =-13 (D)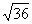 =±6
=±6
28.(12分)如图①,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为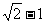 ,直线l:
,直线l: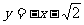 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。
与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。
(1)求点A的坐标及∠CAO的度数;
 (2)⊙B以每秒1个单位长度的速度沿x轴负方向平移,同时,直线l绕点A顺时针匀速旋转。当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切。问:直线AC绕点A每秒旋转多少度?
(2)⊙B以每秒1个单位长度的速度沿x轴负方向平移,同时,直线l绕点A顺时针匀速旋转。当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切。问:直线AC绕点A每秒旋转多少度?

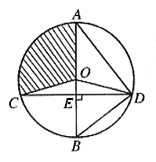
27.(12分)如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。
(1)若,求CD的长;
(2)若 ∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留 )。
)。
26.(12分)亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部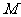 ,颖颖的头顶
,颖颖的头顶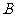 及亮亮的眼睛
及亮亮的眼睛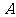 恰在一条直线上时,两人分别标定自己的位置
恰在一条直线上时,两人分别标定自己的位置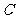 ,
,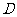 .然后测出两人之间的距离
.然后测出两人之间的距离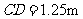 ,颖颖与楼之间的距离
,颖颖与楼之间的距离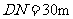 (
(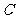 ,
,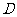 ,
,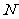 在一条直线上),颖颖的身高
在一条直线上),颖颖的身高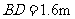 ,亮亮蹲地观测时眼睛到地面的距离
,亮亮蹲地观测时眼睛到地面的距离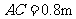 .
.
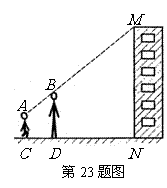 你能根据以上测量数据帮助他们求出住宅楼的高度吗?
你能根据以上测量数据帮助他们求出住宅楼的高度吗?
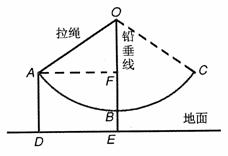
25.(12分)如图,秋千拉绳OB的长为3米,静止时,踏板到地面的距离BE长时0.6米(踏板的厚度忽略不计),小亮荡该秋千时,当秋千拉绳有OB运动到OA时,拉绳OA与铅垂线OE的夹角为55°,请你计算此时该秋千踏板离地面的高度AD是多少米?(精确到0.1米)
24.(10分)已知:630的半径是8,直线烈,PB为oD的切线,A、B两点为切点,
(1)当OP为何值时,∠APB=90°.
(2)若∠APB=50°,求AP的长度(结果保留三位有效数字).
(参考数据si50°=O.7660,cos50°=0.6428,tan50°=1.1918,sin25°=0.4226, COS25°=0.9063,tan25°=O.4663)
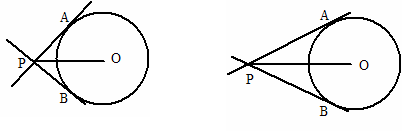
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com