1．骆驼被称为“沙漠之舟”，它的体温随时间的变化而变化，在这一问题中，自变量是(　　 )　　　　　　　　　　　　　　　　　　

A.沙漠　　　　　　　 B.体温　　　　　　　 C.时间　　 　　　　　　D.骆驼

6、作业 基础训练P65-66

5、小结：

角平分线　　　　　　 构造翻折全等。

4、超前突破，提高认识

例4、如图，△ABC中，AB=AC，∠5=100⁰，∠B的平分线

交AC于E，求证：BC=AE+EB

证明：在BC上截取BD=BE，

连结ED。在BD上截取

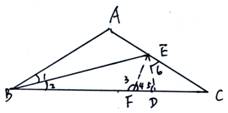BF=BA，连结FE。

∵∠A=100⁰，AB=AC，BE平分∠ABC，

∵∠1=∠2=20⁰

又∵BE=BE　 ∵△ABE≌△FBE　

∴∠3=∠A=100⁰，AE=EF

∴∠4=80⁰ ∵BE=BD，∠2=20⁰， ∴∠5=80⁰

∴∠4=∠5　　 ∴EF-=ED　 ∴AE=ED

又∵∠C=40⁰ ∴∠5=80⁰ ∠6=40⁰ ∴DE=DC

∴AE=DC　　 ∴BC=BD+DC=BE+AE

即BC=AE+EB

3、随堂练习，专题突破

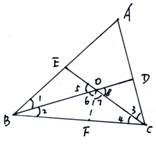例3，如图，△ABC中，∠A=60⁰，两条角平分线BD、CE相交于点O，求证：OD=OE。

证明：在BC上取一点F，

使BF=BE，连结OF。

在△BOE和△BOF中

∵　　 BE=BF

　　　 ∠1=∠2　　　　　 ∴△BOE≌△BOF　 ∴OE=OF，∠5=∠6

　　　 BO=BO

∵∠A=60⁰ ∴∠2+∠4=(180⁰-60⁰)÷2=60⁰

∴∠BOC=180⁰-60⁰=120⁰ ∴∠5=60⁰

∴∠6=∠5=∠8=∠7=60⁰

在△COF和△COD中，

∵　 ∠3=∠4

　　 CO=CO　　　　　　 ∵△COF≌△COD　 ∴OF=OD

　　 ∠7=∠8

∴OD=OE

2、课堂演练，巩固深化

例1、求证，角平分线上的点到角两边

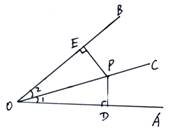的距离相等，如图，已知：OC平分∠AOB，

P切OC上任意一点，PD⊥OA于D，

PE⊥OB于E，求证：PD=PE。

证明：∵PD⊥OA，PE⊥OB

∴∠PDO=∠PEO=90⁰

　　　 ∵OC平分∠AOB　　　 ∴∠1=∠2

在△POD和△POE中，

∵　　　　 ∠PDO=∠PEO

　　　　　 ∠1=∠2 　 　　　　∴△POD△POE　　 ∴PD=PE

　　　　　 OP=OP

例2，如图，△ABC中，∠B=2∠A，AB=2BC。求证：∠A=30⁰。

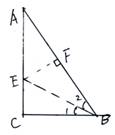证明：作∠ABC的平分线交AC于E。

过E点作EF⊥AB于F。

则∠BFE=∠AFE=90⁰

∵∠ABC=2∠A

∴∠1=∠2=∠A

在△BFE和△AFE中

∵　　　　 ∠2=∠A 　　 ∴△BFE≌△AFE　 ∴BF=AF

　　　　　 ∠BFE=∠AFE

　　　　　 EF=EF

又 ∵AB=2BC　　　 ∴BF=BC

在△BCE和△BFE中

∵　　 BC=BF

　　　　 ∠1=∠2　　　　　 ∴△BCE≌△BFE　 ∴∠C=∠BFE=90⁰

　　　 BE=BE

　　　 ∴∠1=∠2=∠A=30⁰

1、回顾交流，系统跃进。

(1)全等三角形的判定方法有哪些？

(2)判定两个直角三角形全等的方法有哪些？

(3)全等三角形性质是什么？

2、难点：作出正确的辅助线。

1、重点：通过作辅助线，构造“翻折型”全等三角形。

3、培养合情理的能力和创新意识。