(二)新课讲解

1、引入

在四边形中，最常见、价值最大的是平行四边形，如推拉门、汽车防护链、书本等，都是平行四边形，平行四边形有哪些性质呢？

2、平行四边形的定义：

定义：　 两组对边分别平行的四边形叫做平行四边形。

强调：平行四边形首先是一个四边形,但它是一个特殊的四边形，即比一般四边形不同的是：两组对边分别平行。

定义的几何语言表述　 ∵ AB∥CD　 AD∥BC　　 ∴四边形ABCD是平行四边形 。

反过来：∵　 四边形ABCD是平行四边形，

∴　 AB∥ CD，AD∥ BC。

定义的双重性　 具备“两组对边分别平行”的四边形，才是“平行四边形”；反过来，“平行四边形”就一定具有“两组对边分别平行”性质。

平行四边形的表示：用符号　　 表示是一个平行四边形，如　　 ABCD表示平行四边形ABCD。

设问：平行四边形有什么性质呢？边之间有什么关系呢？

活动：让学生看课本上P92探究，用先做好的平行四边形纸板，可量得对边相等。

设问：能否用推理证明这个性质是否成立吗？

(让学生思考本题的已知条件及证明过程)

3、平行四边形的性质：平行四边形的对边相等：

　 前提：是一个平行四边形：

　 结论：这个平行四边形的对边相等。

(提问学生写出已知、求证及证明过程，然后教师加以讲评及纠正。)

　 小结：用几何语言表示：∵四边形ABCD是平行四边形(或在　 ABCD中) ∴ AB=CD，AD=BC。

(一)复习

1、什么是四边形？四边形的一组对边有怎样的位置关系？

2、一般四边形有哪些性质？

　　 一课时。

直尺、三角板、投影仪。

重点：平行四边形的概念和性质1和性质2

难点：平行四边形的性质1和性质2的应用

3．培养学生综合运用知识的能力

2．掌握平行四边形的性质1及性质2、性质3。

1．理解并掌握平行四边形的定义；

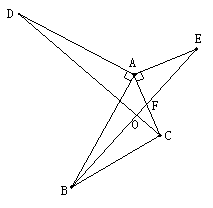
7、(12分)如图所示，已知AB=AD，∠BAD=90°，AC=AE，∠CAE=90°。

求证：(1)CD=BE。(2)∠FOC=90°。

6、(10分)如图所示，已知∠B=∠C=90°，M是BC的中点，DM平分∠ADC。

求证：AM平分∠DAB。