提问学生回答：平行四边形的两组对边有何关系？

设问：对于“平行四边形的对角线互相平分”这个命题，哪些是前提？哪些是结论？

学生回答后教师小结。

分析：这个命题的前提是一个平行四边形，则具有前面学过的性质，结论是两条对角线互相平分。用几何语言表示为：

已知：如图，在平行四边形ABCD中，AC、BD是对角线，且相交与点O，

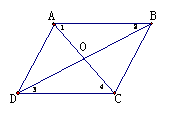求证：AO=CO，BO=DO。

证明： 在平行ABCD中，AB∥ CD，

∴∠1= ∠4 ，∠ 2= ∠3

又∵ AB=CD，

∴ OAB≌OCD(ASA)，

∴ AO=CO，BO=DO。

教师强调“线段互相平分”的意义，讲明表示方法。此题也可证OAD≌OCB得到结论，教师可多方面启发。

强调：同学们归纳的关于平行四边形的边、角、对角线的关系的命题，通过推证都是正确的，今后我们可以直接应用这些性质。其中，教材把“对角相等”“对边相等”、“对角线互相平分”作为性质定理。

教师小结：

性质定理1：平行四边形的对角相等；

性质定理2：平行四边形的对边相等；

性质定理3：平行四边形的对角线互相平分。

随堂练习：(提问回答)

1、◇ABCD中，已知AB=a，BC=b，

∠A=50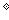，那么◇ABCD的周长为 (　　 )，∠B=(　 )，∠C=(　 )，∠D=(　　 )。

(一)请同学们观察图一(课件中，定义、图、按纽)，首先有几条边？找出对边、对角、邻边、邻角、对角线。

在上图中，当AB∥CD，AD∥BC时，四边形ABCD就是平行四边形。(课件打出定义)

(五)作业布置：

(1)课本P100第2题

(2)在平行四边形ABCD中，若∠A：∠B=2：3，求∠C、∠D的度数。

19.1.1平行四边形的性质(三)

教学目的：

1、掌握平行四边形的概念，会用定义识别平行四边形。

2、掌握平行四边形对边相等、对角相等的基础上，掌握对角线互相平分的性质，初步会运用这些性质进行有关的论证和计算。

3、渗透从具体到抽象化未知为已知的数学思想及事物之间相互转化的辨证唯物主义观点。

教学重点：掌握对角线互相平分的性质。

教学难点：探索、寻求解决问题的思路

教学用具：投影仪、模型。

教学过程：

(四)本课小结：平行四边形除了对边平行且相等外，其对角也相等。

(二)新课讲解

　 设问：平行四边形除了对边平行、对边相等之外，还有什么性质呢？

　　 活动：课本P92，用做好的平行四边形纸模，量一量平行四边形对角是否相等。

　　 小结：平行四边形的对角相等，

　　 设问：如右图中，哪些是对角？

　　 答：∠A与∠C，∠B与∠D。

用几何语言表达：∵四边形ABCD是平行四边形

(或在　 ABCD中) ∴ ∠A=∠C，∠B=∠D 。

设问：能否用证明方法证明命题的正确的呢？

让学生写出已知、求证、证明过程。(教师加以纠正讲评)

随堂练习：

(1)课本P93练习第2题(提问回答)

(2)在平行四边形ABCD中，∠A=50⁰，求∠B、∠C、∠D的度数。

(3)在平行四边形ABCD中，∠A=∠B+240，求∠A的邻角的度数

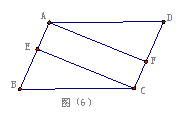(三)例题讲解：如图，在平行四边形ABCD中，AE=CF，求证AF=CE

分析：要证明AF=CE，只要证

ΔADF≌ΔCBE，但这两个三角形全等的

条件充分吗？

　　 证明：在　　 ABCD中，AD=CB，∠B=∠D，AB=CD

　　　　　 ∵ AE = CF

　　　　　 ∴ AB-AE=CD-CF

　　　　　 即 BE=DF

　　　　　 ∴ ΔADF≌ΔCBE

　　　　　 ∴ AF=CE

练习：练习册

(一)复习

1．什么样的四边形是平行四边形？

2．平行四边形的性质中，我们学过什么性质？

(2)如图，AD∥BC，AE∥CD，BD平分∠ABC，

求证AB=CE

19.1.1平行四边形及其性质(二)

教学目的：

1、掌握平行四边形的概念，会用定义识别平行四边形。

2、掌握平行四边形对边相等、对角相等的性质，初步会运用这些性质进行有关的论证和计算。

3、渗透从具体到抽象化未知为已知的数学思想及事物之间相互转化的辨证唯物主义观点。

4、培养观察、分析、归纳、概括能力。

教学重点：平行四边形的概念和性质

教学难点：探索、寻求解决问题的思路

教学用具：

直尺、三角板、投影仪。

教学时间：

　　 一课时。

教学过程

两组对边分别平行的四边形是平行四边形，平行四边形对边平行且相等。

分析：用平行四边形的对边相等，得一组邻边之和等于周长的一半，可得邻边AB+BC =36/2=18，又已知AB=8，可得BC的长，其它两边的长与这两边之长相同。

练习：课本P93练习题1、3(第1题让学生板书，第3题提问)

巩固练习(用投影投出)：

平行四边形的两邻边的比是2：5，周长为28cm，求四边形的各边的长。