1．课本P101第10，选做：课本P132第9题2．练习册相关内容。

　　 今天我们主要研究了利用边的关系来判定平行四边形，注意满足两个条件。

　　 注意：若一组对边平行，另一组对边相等，是不可以判定为平行四边形的，它是梯形。

例1：已知：E、F分别为平行四边形ABCD两边

AD、BC的中点，连结BE、DF

　　 求证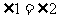：　　　　　　　　　　　　　　　　 图3

分析：今天我们证明角相等，除了平行线，全等三角形外，又多了一个新方法，可以证明平行四边形对角相等，即只要四边形EBFD是平行四边形。由已知平行四边形ABCD的性质可得DE//BF，又AD＝BC，E、F为中点则有DE＝BF，根据“一组对边平行且相等的四边形是平行四边形”的判定定理，可得四边形EBFD是平行四边形。

　 　证明由学生完成。

　　 提问：此题还有什么方法，证明四边形BEDF是平行四边形。学生会想到证明，得到BE＝DF，利用两组对边相等证明四边形是平行四边形。但应指出第二种方法较第一种方法繁，也就是说要找出较简捷的证法，准确地使用判定定理，就要先分析图形的性质，及所具备的条件。

练习：课本P99练习第2及课本P100习题第4题(让两位学生板演证明的过程，教师加以讲评。)

设问：若一个四边形有一组对边平行且相等，能否判定这个四边形也是平行四边形呢？

活动：课本P97探究内容，并用事准备好的纸条(纸条的长度相等)，先将纸条放置不平行位置，让学生设想若二纸条的端点为四边形的顶点，则组成的四边形是不是平行四边形？若将纸条摆放为平行的位置，则同样用二纸条的端点为顶点组成的四边形是不是平行四边形？

设问：我们能否用推理的方法证明这个命题是正确的呢？(让学生找出题设、结论，然后写出已知、求证及证明过程。)

小结：平行四边形判定方法五：

前提：若一个四边形有一组对边平行且相等。

结论：这个四边形是一个平行四边形。

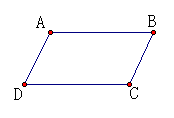
如图用几何语言表达为：

∵AB=CD 且AB∥CD

∴四边形ABCD是平行四边形

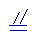
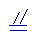平行且相等可用符号“　 ”，读作“平行且相等”。

∵AB　 CD

∴四边形ABCD是平行四边形

　　 (1)．我们已学过哪些方法来判定一个四边形的平行四边形？(提问回答)

3、在教学中渗透事物总是相互联系又相互区别的辨证唯物主义观点。

教学重点：掌握用“一组对边平行且相等的四边形是平行四边形”这一判定定理来判定一个四边形是平行四边形。

教学难点：判定定理的证明方法及运用。

教学用具：二对长度相等的纸条、尺、投影仪等。

教学时间：一课时。

教学过程：

2、培养学生的观察能力、动手能力自学能力、计算能力、逻辑思维能力；

1、掌握“一组对边平行且相等的四边形是平行四边形”这一判定定理进行有关的论证和计算；

19．1．2平行四边形的判定(三)

教学目的：

1、熟记“判定定理3”；　　 2．课本P100第4、9题。3、完成练习册。