
(五)作业
1. 已知:矩形ABCD,M是BC的中点,BC=2AB。求证: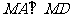 。
。
2. 矩形的对角线的一个交角是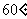 ,一条对角线长为8cm。求矩形的边长。
,一条对角线长为8cm。求矩形的边长。
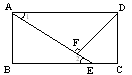
3. 已知:如图7,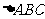 的两条高线BE、CF;M为BC中点,N为EF中点。求证:
的两条高线BE、CF;M为BC中点,N为EF中点。求证: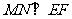 。
。
19.2.1 矩形(四)
教学目标:
1.使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力
2.通过矩形判定的教学渗透矛盾可以互相转化的唯物辩证法思想
教法设计:
观察、启发、总结、提高,类比探讨,讨论分析,启发式.
教学重点:矩形的判定.
教学难点:矩形的判定及性质的综合应用.
课时安排:1课时
教具学具准备:教具(一个活动的平行四边形),投影仪及胶片。
教学步骤:
(四)小结
今天我们主要学习了矩形的定义及性质,矩形是角特殊的平行四边形,决定了矩形的四个角都是直角,对角线相等。由于矩形的对角线把矩形分割成直角三角形,等腰三角形,所以我们还要把直角三角形,等腰三角形,等边三角形的性质、判定好好复习一下,这对于解决矩形问题是大有好处的。
(三)巩固练习
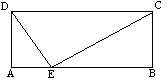
 1. 如图5,在矩形ABCD中,
1. 如图5,在矩形ABCD中,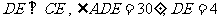 ,求这个矩形的周长。(答案:16+
,求这个矩形的周长。(答案:16+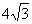 )
)
图5 图6
在矩形中若存在矩形对角线,那就一定要利用矩形对角线的性质,即相等又平分,转化成等腰三角形,利用等边对等角的性质。
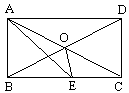
2. 已知:如图6,矩形ABCD中,AE平分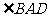 交BC于E,若
交BC于E,若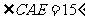
求: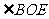 的度数。(提示:要充分利用等腰
的度数。(提示:要充分利用等腰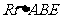 ,等边
,等边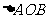 的性质)
的性质)
(一)复习、引入
提问:1. 什么叫平行四边形?学生回答后强调任何定义都具有可逆性,即是定义,又是判定。)
2. 叙述平行四边形的性质和判定定理,(再强调分析命题的条件与结论的关系)。
3.矩形具有什么性质?直角三角形有什么特殊性质?
 (二)新课讲解:
(二)新课讲解:
已知:如图2,矩形ABCD中,E是BC上
一点,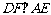 于F,若
于F,若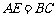 。求证:CE=EF。
。求证:CE=EF。
图2
 分析:CE、EF分别是BC,AE等线段上的一部分,若AF=BE,则问题解决,而证明AF=BE,只要通过
分析:CE、EF分别是BC,AE等线段上的一部分,若AF=BE,则问题解决,而证明AF=BE,只要通过 ,在矩形中容易构造全等的直角三角形。(板书证明过程)
,在矩形中容易构造全等的直角三角形。(板书证明过程)
已知:如图3,矩形ABCD中,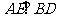 于E,
于E,
且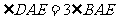 。
。
求: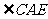 的度数。
的度数。
分析:由已知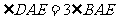 可得
可得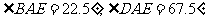 。而所求
。而所求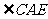 是
是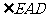 的一部分,就要研究
的一部分,就要研究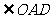 与其它角的关系。因为OA=OD,所以
与其它角的关系。因为OA=OD,所以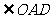 =
=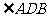 。把题目中的已知条件
。把题目中的已知条件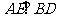 ,与矩形的性质
,与矩形的性质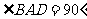 结合起来,得到基本图形直角三角形斜边上的高的形式,可以推出
结合起来,得到基本图形直角三角形斜边上的高的形式,可以推出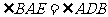 ,于是得到
,于是得到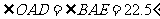 ,求
,求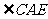 的度数也就显然了。(板书讲明过程)
的度数也就显然了。(板书讲明过程)
19.2.1 矩形(三)
教学目的:
使学生掌握矩形的定义和性质,理解并掌握矩形和平行四边形的联系和区别,使学生能应用以上知识解决有关问题,培养学生的逻辑推理能力。
教学重点:掌握矩形的性质
教学难点:利用矩形的性质解决问题
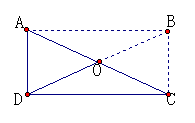 活动:用先准备好的矩形纸模,先矩形沿对角线对折,得到一个直角三角形(如下图1),由矩形对角线的性质,可得点O
活动:用先准备好的矩形纸模,先矩形沿对角线对折,得到一个直角三角形(如下图1),由矩形对角线的性质,可得点O
是AC的中点,得DO是AC边的中线。
设问:中线DO的长度与对角线 AC的长度有
何关系?对AO、CO有何关系呢?
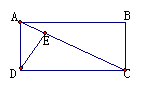 结论:AO=DO,DO=CO,DO=
结论:AO=DO,DO=CO,DO=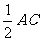 ,
,
即直角三角形斜边上的中线等于斜边的一半。
例题讲解:课本P113
分析:可作斜边AB的中线CD,则得CD=DA=DB=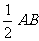 ,又已知AB=2AC,得三角形DCA是等边三角形,得∠A=60°,可得∠B=30°。
,又已知AB=2AC,得三角形DCA是等边三角形,得∠A=60°,可得∠B=30°。
综合应用练习:
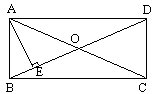
如图1,E为矩形ABCD对角线AC上一点,
DE⊥AC于E,∠ADE: ∠EDC=2:3,求∠BDE的度数.
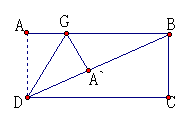 如图2,折叠矩形ABCD纸片,
如图2,折叠矩形ABCD纸片,
先折出折痕BD,再折叠使A落在对角线BD
上A′位置上,折痕为DG。AB=2,BC=1。
求AG的长。(答5-12)。
3.练习册相应内容。
3.矩形的性质的内容是什么?
2.矩形的对角线有什么特点呢?
1.矩形的角有什么特点呢?
3.利用直角三角形这一性质进行计算和证明。
教学重点:矩形的性质定理及“直角三角形斜边上的中线等于斜边的一半”这一性质;
教学难点:利用直角三角形这一性质进行计算和证明。
教学方法:讨论法、启发法、 练习法、类比法。
教学用具:小黑板、投影仪、圆规、三角板、纸模。
教学过程:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com