
1.提问:我们已经学习了矩形的性质,矩形有哪些性质呢?
3、在教学中渗透事物总是相互联系又相互区别的辨证唯物主义观点。
教学重点:菱形定义及其性质。
教学难点:性质的证明方法及运用。
教学程序:
1、理解并掌握菱形的定义及性质2;会用这些定理进行有关的论证和计算;
讲评练习题
讲评内容:练习册矩形部份的相应的练习题
讲评时间:一课时。
19.2.2菱形的性质(一)
教学目的:
(2)要注意不要不加考虑地把性质定理的逆命题作为矩形的判定定理.
3.矩形知识的综合应用。(让学生思考,然后师生共同完成)
 例:已知
例:已知
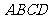 的对角线
的对角线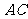 ,
,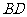 相交于
相交于
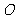 ,△
,△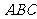 是等边三角形,
是等边三角形, ,求这个平行
,求这个平行
四边形的面积(图2).
分析解题思路:(1)先判定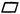
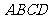 为矩形.(2)求出
为矩形.(2)求出 △
△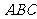 的直角边
的直角边 的长.(3)计算
的长.(3)计算 .
.
2.矩形判定方法的实际应用
除教材中所举的门框或矩形零件外,还可以结合生产生活实际说明判定矩形的实用价值.
设问:1.矩形的判定.
2.矩形是有一个角是直角的平行四边形,在判定一个四边形是不是矩形,首先看这个四边形是不是平行四边形,再看它两边的夹角是不是直角,这种用“定义”判定是最重要和最基本的判定方法(这体现了定义作用的双重性、性质和判定).除此之外,还有其它几种判定矩形的方法,下面就来研究这些方法.
方法1:有三个角是直角的四边形是矩形.(并让学生写出推理过程。)
矩形判定方法2:对角钱相等的平行四边形是矩形.(分析判定方法2和学生一道写出证明过程。)
归纳矩形判定方法(由学生小结):
(1)一个角是直角的平行四边形.(2)对角线相等的平行四边形.
(3)有三个角是直角的四边形.
3.矩形与平行四边形有什么共同之处?有什么不同之处?
2.矩形有哪些性质?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com