
2.补充练习:如图4,已知正方形ABCD,延长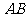 到
到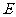 ,
,
连结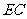 ,作
,作 于
于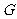 ,
,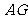 交
交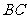 于
于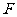 ,求证:
,求证: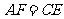 .
.
2.正方形的性质
因为正方形是特殊的平行四边形,还是特殊的矩形,特殊的菱形,所以它具有这些图形性质的综合,因此正方形有以下性质(由学生和老师一起总结).
正方形性质定理1:正方形的四个角都是直角,四条边相等.
正方形性质定理2:正方形的两条对角钱相等并且互相垂直平分,每一条对角线平分一组对角.
说明:定理2包括了平行四边形,矩形,菱形对角钱的性质,一个题设同时有四个结论,这是该定理的特点,在应用时需要哪个结论就用哪个结论,并非把结论写全.
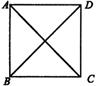 例题讲解:例4 如图3,(按课本方式板书)
例题讲解:例4 如图3,(按课本方式板书)
|
设问:矩形和菱形都是特殊的平行四边形,那么更加特殊的平行四边形是什么图形?它又有什么特殊性质呢?这一堂课就来学习这种特殊的图形--正方形(写出课题)
1.正方形的定义:有一组邻边相等,有一个角是直角的平行四边形叫做正方形.
设问:正方形从定义看,它既是矩形又是菱形。哪么它又有什么性质呢?
2.说明平行四边形、矩形、菱形的内在联系.
1.让学生叙述平行四边形、矩形、菱形的定义和它们的特殊性质.
3.正确运用正方形的性质解题.
教学方法:小结、归纳、提高
教学重点:正方形的性质.
教学难点:正方形性质的应用.
课时安排:1课时
教具学具准备:投影仪、胶片、多媒体、常用画图工具
教学过程:
2.掌握正方形的性质定理.
1.掌握正方形的定义,理解正方形与平行四边形、菱形、矩形的关系.
讲评练习题
讲评内容:练习册菱形部份的相应的练习题
讲评时间:一课时。
19.2.3 正方形(一)
教学目的:
设问:(1)菱形的定义能否作为菱形的判定?有哪两个条件?
 (2)有什么方法来判定一个四边形是菱形?
(2)有什么方法来判定一个四边形是菱形?
活动:课本P109“探究”
小结:对角线互相垂直的平行四边形是菱形。
提问:这个命题的前提是什么?结论是什么?
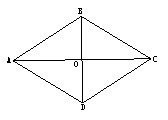
已知:在平行四边形ABCD中,对角线AC⊥BD,
求证:平行四边形ABCD是菱形。
分析:我们可根据定义来证明这个四边形是平行四边形,由平行四边形的性质得到BO=DO,由∠AOB=∠AOD=90º及AO=AO,得ΔAOB≌ΔAOD,可得到AB=AD,得平行四边形ABCD是菱形。(I板书证明过程。)
方法二:四边相等的四边形的菱形。
设问:如何证明这个命题呢?(让学生思考并证明)
几何证言表达:在四边形ABCD中,AB=BC=CD=DA,
∴四边形ABCD是菱形。
小结:(1)菱形判定方法,填写下表。
|
|
应具备两个条件 |
|
|
菱形的定义 |
|
|
|
菱形判定方法一(定义) |
|
|
|
判定方法1 |
|
|
|
判定方法2 |
|
|
练习:(1)对角线互相垂直的四边形是菱形。( )
(2)对角线互相平分的四边形是菱形。( )
(3)两组对边分别平行,且对角线 的四边形是菱形。
(4)两组对边分别相等,且对角线互相垂直的四边形是菱形。( )
综合应用练习
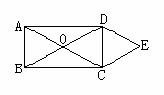 (1)如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E,求证:四边形OCED是菱形。
(1)如图,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD,DE和CE相交于E,求证:四边形OCED是菱形。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com