4．总结本章常用的数学思想方法，提高逻辑思维能力．

重点：平行四边形与特殊平行四边形的从属关系及它们的概念、性质和判定方法．

难点：提高数学思维能力．

教学过程：

理解本章基本图形的形成、变化和发展过程

本章知识结构图，如图

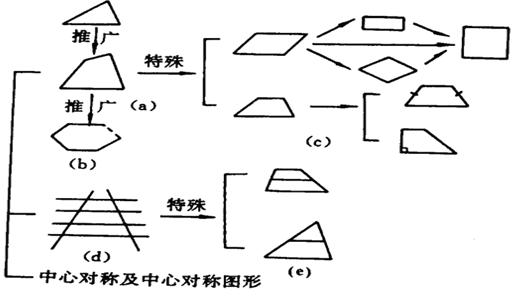
说明：

(1)图4-107(c)中要求各种特殊四边形的概念、性质、判定和它们之间的关系；

(2)图4-107(d)中要求平行线等分线段定理的内容，会任意等分一条已知线段；

(3)图4-107(e)中要求三角形、梯形中位线的概念、性质、判定；

3．总结常用添加辅助线的方法．

2．对比掌握各种特殊四边形的概念，性质和判定方法．

1．利用基本图形结构使本章内容系统化．

3．多边形面积的计算原则(分割)．

作业：

讲评练习题

讲评内容：练习册梯形部份的相应的练习题

讲评时间：一课时。

全章回顾与思考

教学目标

2．梯形中位线的定义、性质与判定．

3．梯形、多边形面积的计算

小学学过的梯形面积S=(a+b)h÷2 ，而l=(a+b)÷2，推出S=lh(l为梯形中位线长，h为梯形高)．

多边形面积的求法，任意多边形面积可以通过辅助线，把它分割成三角形、平行四边形、梯形，就可以利用这些图形的面积公式计算任意多边形面积．

例2 有一块四边形的地ABCD，(图4－68)，

测得AB=26m，BC=10m，CD=5m，顶点B、C到AD

的距离分别为10m、4m，求这块地的面积．

分析：解题的关键是通过辅助线把多边

形分割成面积可以计算的常见图形(三角形、平行四边形、梯形等)，至于解答程序可不作限制．可以先列出所求面积公式，再求公式中的未知项，最后代入公式求出结果；也可以先列出已知项，求出有关的未知项，再列出公式，将数值代入求出结果．

小结：1．三角形中位线定义、性质与判定．

2. 等腰梯形的常用辅助线的添加方法

作法一：过点C作CF∥AD交AB延长线于F

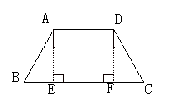作法二：过A作AF⊥DC于F，BE⊥DC于E

作法三：延长DA、CB交于点O　 　　　　　　　　　　作法二

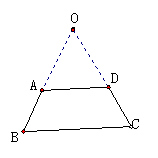
作法四： 过点B作 BE∥AD，交DC于点

作法五：过点B作BE∥AC交DC延长线于点E

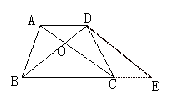
　　　　　 作法四　　　　　　　 作法五

1．梯形中位线

设问：什么是梯形的中位线呢？

(结合图形介绍)定义：连结梯形两腰中点的线段叫做梯形的中位线．

强调：梯形中位线是连结两腰中点的线段，而不是连结两底中点的线段．

练习：课本P121习题第9题(让学生思考并寻求证明方法，教师加以巡视及点拨。)

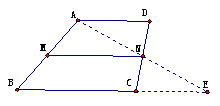
分析：如图，连AN并延长交BC延长线于

E，这样可证△ADN≌△ECN,得AD=CE，MN变

成△ABE的中位线，可得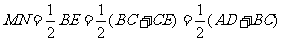,且有

MN∥BC∥AD

小结：1.梯形中位线性质：梯形中位线平行于两底，并且等于两底和的一半．该定理的证明关键是如何添加辅助线，把梯形中位线转化成三角形的中位线．

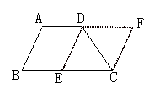
2．如图，等边三角形各边中点的连线形成什么图形？