活动一：向学生简略介绍物体重力的产生和重心的含义。

活动二：探究小木条的重心。

结论：重心在小木条所在线段的中点上。

活动三：用带线的重锤与平行四边形及特殊的平行四边形有同一顶点挂起来，找到重力的作用线，这样做二次，得到二条重力作用线的交点，即为平行四边形的重心。

结论：平行四边形的重心是它的对角线的交点。

活动四：探究三角形的重心(让学生自己动手按活动三的方法做，找出三角形的重心)

小结：三角形的重心在三角形三条边的中线的交点上。

活动五：让学按照刚才的方法寻找任意四边形的重心的位置。

3．了解重心的物理意义，体会数学与物理之间的联系，能用实验方法寻找任意多边形的重心。

教学重点：通过课题学习的任务、目的、结论等环节，培养学生探究能力和创新意识。

教学难点：实验活动的规范操作，及寻找三角形的重心。

教学用具：平行四边形、特殊平行四边形纸模，三角形纸模，一小段木条，带线的重锤等。

教学时间：一课时。

教学过程。

2．在探索线段、特殊平行四边形、三角形、任意多边形的重心活动等过程，让学生经历观察、实验、猜想等过程，发展几何直觉。

1．通过寻找几何图形的重心的数学活动，经历探究物体与图形的重心的过程，了解规则几何图形的重心就是它的几何中心。

19.4 课题学习　 重心

教学目的

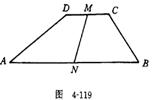
3.已知：如图4-119，梯形ABCD中，DCAB，ㄥA+AB=90°，M，N分别为CD，AB点.求证：MN=12(AB-CD).

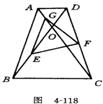
2.如图4-118，梯形ABCD中，ADBC，AB=CD，E，F和G分别为OB，CD，OA中点，ㄥAOD=60°.求证：△EFG是等边三角形.

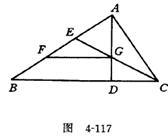
1.已知：如图4-117，Rt△ABC中，ㄥACB的平分线交对边于E，交斜边上的高AD于G，过G作FGCB交AB于F.求证：AE=BF.

2.基本思想及观点：

(1)“特殊--一般--特殊”认识事物的方法；

(2)集合、方程、分类讨论及化归的思想；

(3)用类比、运动的思维方法推广命题.

1.基本方法.

(1)利用基本图形结构使知识系统化；

(2)证明两条线段相等及和差关系的方法，也可类比总结证明两角相等，角的和差、倍、分问题，直线垂直、平行关系的方法；

(3)利用变换思想添加辅助线的方法；

(4)探求解题思路时的分析、综合法.