
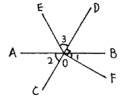
5.如图所示,已知直线AB,CD相交于O,OE平分∠AOD,FO⊥OD于O,∠1=40°,则∠2=____,∠3=____。
21,长方体木盒是左右侧面积为12cm2的正方形,下底面的面积18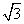 cm2,求该长方体的长是多少?
cm2,求该长方体的长是多少?
22,分别求出下列各数在哪两个整数之间.
(1)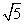 ; (2)
; (2)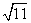 ; (3)
; (3)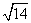 ; (4)
; (4)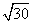 .
.
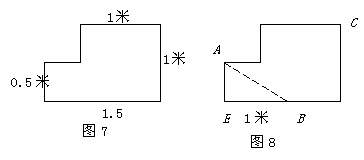
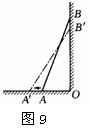
23,木匠王师傅在做家具时遇到一块不规则的木板(如图7),现需要将这块木板锯开后胶合成一正方形王师傅已锯开一线(如图8),请你帮他再锯一线然后拼成正方形.想想看,在锯拼过程中王师傅用到了什么运动变换?
24,当x=2,y=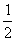 时,求代数式 (x+y)(x-y) + (x-y)2-(x2-3xy)的值.
时,求代数式 (x+y)(x-y) + (x-y)2-(x2-3xy)的值.
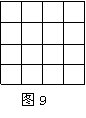
25,如图9,正方形网格中的每个小正方形边长都是1,任意连结这些小正方形的顶点,可得到一些线段.请在图中画出AB=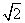 ,CD=
,CD=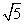 ,EF=
,EF=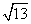 ,这样的线段,并选择其中的一个说明这样画的道理.
,这样的线段,并选择其中的一个说明这样画的道理.
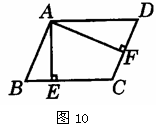
26,如图10,在□ABCD中,AE⊥BC,AF⊥CD,垂足分别为E、F,若AE=4,AF=6,□ABCD的周长为40,求平行四边形ABCD的面积S等于多少?
27,若有三个村庄A、B、C之间的距离分别为AB=5km,BC=12km,AC=13km.要从B修一条公路BD直达AC.已知公路的造价为26000元/km,求修这条公路的最低造价是多少?
28,如图11,(1)分别观察甲组4个小题中的图形,看看每小题中的深色三角形是经过怎样的变换,变成浅色三角形的,并将各小题图形变换的规律填在横线上.(如,平移变换,旋转变换,中心对称,轴对称或几种变换的组合)
(2)按照你找出的甲组中各小题图形变换规律,将乙组对应小题中的图形进行相应的变换,并用阴影表示出变换后的图形.(即用甲组第1小题的图形变换规律,将乙组第1小题的图形变换,并画出图形,依次类推)
 甲组:
甲组:
变换规律:1. 2. 3. 4.
 乙组:
乙组:
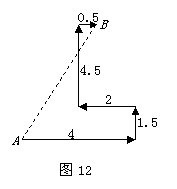
29,如图12所示,某人到岛上去探宝,从A处登陆后先往东走4km,又往北走1.5km,遇到障碍后又往西走2km,再折回向北走到4.5km处往东一拐,仅走0.5km就找到宝藏。问登陆点A与宝藏埋藏点B之间的距离是多少?
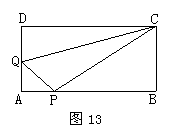
30,如图13,在矩形ABCD中,AB=12cm,BC=6cm.点P沿AB边从点A开始向B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t表示时间(0≤t≤6),那么(1)当t为何值时△QAP为等腰三角形.(2)求四边形QAPC的面积?并提出一个与计算结果有关的结论.
11,计算:(-3a)3 ·(-a3)2 = .
12,分解因式:5a3-125a=_________.
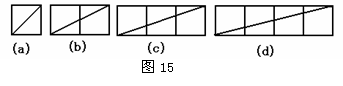
13,如图3所示,左图变成右图的过程是________.


14,如图4,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是_______,旋转了______度.
15,小明的房间面积为10.8m2,房间地面恰好是由120块相同的正方形地砖铺成的,则每块地砖的边长是________m.
16,等边△ABC的高为3cm,以AB为边的正方形面积为 .
17,在△ABC中,∠C=90°,BC=60cm,CA=80cm,一只蜗牛从C点出发,以每分20cm的速度沿CA→AB→BC的路径再回到C点,需要 分的时间.
18,若一个三角形的三边之比为5∶12∶13,且周长为60cm,则它的面积为 .
19,如图5,是2002年8月北京第24届国际数学家大会会标,由4个全等的直角三角形拼合而成.如果图中大、小正方形的面积分别为52和4,那么一个直角三角形的两直角边的和等于 .
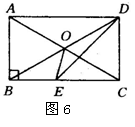
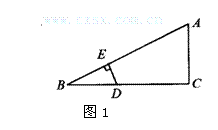
20,如图6所示,在矩形ABCD中,对角线交于点O,DE平分∠ADC,∠AOB=60°,则∠COE=_______.
1,下列各式能分解因式的是( )
A.x-y B.x2+1 C.x2+y+y2 D.x2-4x+4
2,下列多项式相乘,不能运用公式“(a+b)(a-b)=a2-b2”计算的是( ) A.(2x-y)(2x+y) B.(-2x-y)(-2x+y) C.(-2x-y)(2x+y) D.(-2x+y)(2x+y)
3,若 +│8b-3│=0,则ab的值为( )
+│8b-3│=0,则ab的值为( )
A.8 B.1 C.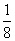 D.
D.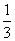
4,下列语句正确的是( )
A.一个数的立方根不是正数就是负数
B.负数没有立方根
C.如果一个数的立方根是这个数本身,那么这个数一定是零
D.一个数的立方根与这个数同号,零的立方根是零
5,矩形、菱形、正方形都具有的性质是( )
A.对角线相等 B.对角线互相垂直 C.对角线平分一组对角 D.对角线互相平分
 6,如图1所示的两个圆,其中圆C是由圆D旋转得到的,则它的旋转中心的个数是( )
6,如图1所示的两个圆,其中圆C是由圆D旋转得到的,则它的旋转中心的个数是( )
A.1 B.2 C.3 D.无数个

7,一个扇形( )
A.是轴对称图形,但不是旋转对称图形 B.是旋转对称图形,但不是轴对称图形
C.是轴对称图形,也是旋转对称图形 D.既不是轴对称图形,也不是旋转对称图形
8,如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )
A.7,24,25 B.3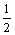 ,4
,4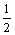 ,5
,5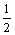 C.3,4,5 D.4,7
C.3,4,5 D.4,7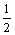 ,8
,8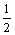
9,放学以后,小红和小颖从学校分手,分别沿东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖20分钟到家,小红和小颖家的直线距离为( )
A.600米 B. 800米 C. 1000米 D. 不能确定
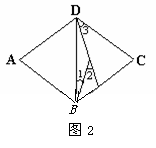
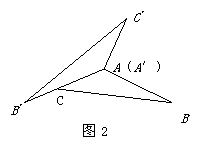
10,已知菱形ABCD,∠A=72°,将它分割成如图2所示的四个等腰三角形,则∠1,∠2,∠3,的度数分别是( )
A.36°,54°,36° B.18°,54°,54° C.18°,36°,36° D.54°,18°,72°
21,已知(x+y)2=1,(x-y)2=11.求:
(1)x,y两数的平方和;(2)x,y两数的积.
22,若x、y都是实数,且y=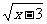 +
+ +8,求x+3y的立方根.
+8,求x+3y的立方根.
23,已知5+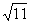 的小数部分为a,5-
的小数部分为a,5-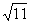 的小数部分为b,求:
的小数部分为b,求:
(1)a+b的值;
(2)a-b的值.
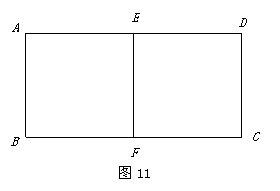 24,如图11,四边形ABEF与四边形EFCD是两个大小一样的正方形,试找出图中所有能使正方形EFCD按顺时针方向旋转一定角度后能与正方形ABFE重合的点(可另设字母),并分别说出旋转的度数.
24,如图11,四边形ABEF与四边形EFCD是两个大小一样的正方形,试找出图中所有能使正方形EFCD按顺时针方向旋转一定角度后能与正方形ABFE重合的点(可另设字母),并分别说出旋转的度数.
 25,某村有一个呈四边形的池塘,在它的四个角A,B,C,D处均种有一棵枣树,这个村准备利用池塘建养鱼池,既想使池塘面积扩大一倍,又想保住枣树不动,并要求扩建后的池塘成平行四边形形状,问该村能否实现这一设想.若能,请你设计并画出图形;若不能,请说明理由.
25,某村有一个呈四边形的池塘,在它的四个角A,B,C,D处均种有一棵枣树,这个村准备利用池塘建养鱼池,既想使池塘面积扩大一倍,又想保住枣树不动,并要求扩建后的池塘成平行四边形形状,问该村能否实现这一设想.若能,请你设计并画出图形;若不能,请说明理由.
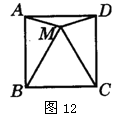
26,如图12所示,正方形ABCD中,M是正方形内一点,且为等边三角形,连结MA、MD,将ΔADM绕点D顺时针旋转多少度才能使AD与DC重合?标出点M的对应点M′的位置,猜想ΔDMM′是什么三角形?
27,任意剪一个梯形纸片,利用对折的方法找到腰的中点E、F,按图13中所示的方法分别将含∠A,∠B的部分向里剪下①,②,并按图中箭头所示的方向旋转180°,
①你能得到一个怎样的四边形?
②你能发现关于线段EF的哪些特性?
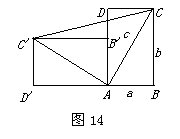 ③请你画出一条直线,将梯形ABCD分成面积相等的两部分(保留作图痕迹),这样的直线你能画几条?简要说明你的想法.
③请你画出一条直线,将梯形ABCD分成面积相等的两部分(保留作图痕迹),这样的直线你能画几条?简要说明你的想法.
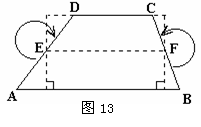
28,一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图14,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积验证勾股定理:a2+b2=c2.
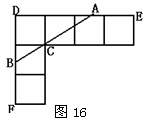
29,已知:正方形的边长为1.(1)如图15(a),可以计算出正方形的对角线长为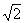 .图(b),求两个并排成的矩形的对角线的长.n个呢?(2)若把(c)(d)两图拼成如图16“L”形,过C作直线交DE于A,交DF于B.若DB=
.图(b),求两个并排成的矩形的对角线的长.n个呢?(2)若把(c)(d)两图拼成如图16“L”形,过C作直线交DE于A,交DF于B.若DB=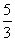 ,求DA的长度.
,求DA的长度.
30,如图17,在△ABC中,∠ACB=90º,AC=BC,P是△ABC内的一点,且PB=1,PC=2,PA=3,求∠BPC的度数.

11,一个3 次单项式与一个4次单项式相乘,积是 次单项式.
12,已知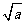 =1.2,则a=_______;
=1.2,则a=_______; 的算术平方根是________.
的算术平方根是________.
13,将勾股数3,4,5扩大2倍,3倍,4倍,…,可以得到勾股数6,8,10;9,12,15;12,16,20;…,则我们把3,4,5这样的勾股数称为基本勾股数,请你也写出三组基本勾股数 , , .
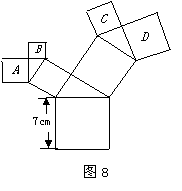 14,如图6所示,把△ABC绕点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A=_______.
14,如图6所示,把△ABC绕点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A=_______.
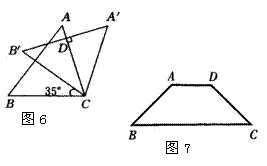
15,如图7,梯形ABCD中,AD∥BC,AB=CD,∠B=45°,它的高为2,上底与下底之和为10,则上底AD等于_________.
16,若一个三角形的三边a、b、c满足a2+b2+c2-ab-bc-ca=0,则该在三角形为 .
17,如图8,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积之和为_______cm2.
18,如图9,梯子AB靠在墙上,梯子的底端A到墙根O的距离为2米,梯子的顶端B到地面的距离为7米.现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根O的距离等于3米,同时梯子的顶端 B下降至 B′,那么 BB′的值: ①等于1米;②大于1米5;③小于1米.其中正确结论的序号是 .
 19,如图10,正方形ABCD与正方形OEFG的面积分别是9cm2和16cm2.O是正方形ABCD的中心,则图中阴影部分的面积是 cm2.
19,如图10,正方形ABCD与正方形OEFG的面积分别是9cm2和16cm2.O是正方形ABCD的中心,则图中阴影部分的面积是 cm2.
20,把两个全等的非等腰三角形拼成平行四边形,可拼成的不同平行四边形的个数为_____个.
1,如果多项式x2+mx+16恰好能分解为一个二项式的平方的形式,那么m的值为( ) A.4 B.8 C.-8 D、±8
2,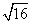 的平方根是( )
的平方根是( )
A.-4 B.4 C.±4 D.不存在
3,已知一个直角三角形的两边长分别为3和4,则第三边长是( )
A.5 B.25 C.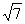 D.5或
D.5或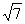
4,若二次三项式x2+ax-1可分解为(x-2)(x+b),则a+b的值为( )
A.-1 B.1 C.-2 D.2
5,如图1所示,在△ABC中,∠C=90°,D为BC边的中点,DE⊥AB于E,则AE2-BE2等于( )
A.AC2 B.BD2 C.BC2 D.DE2
6,如图2,△ABC按顺时针旋转一个角后成为△A′B′C′,指出哪一点是旋转中心( )
A.点A B.点B C.点C D.点B′
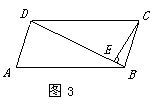
7,如图3,在平行四边形ABCD中,BD=CD,ÐA=70°,CE^BD于E,则ÐBCE等于( )
A.20° B.25° C.30° D.35°
8,如图4所示,在△ABC中,三边a,b,c的大小关系是( )
A.a<b<c B. c<a<b C. c<b<a D. b<a<c


9,计算:(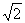 -
-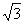 )2006·(
)2006·(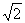 +
+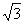 )2007的结果是( )
)2007的结果是( )
A.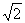 +
+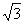 B.
B.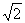 -
-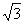 C.
C. 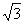 -
-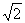 D.
D.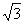
10,如图5所示,已知△ABC和△DCE都是等边三角形,图中的三角形,可以通过旋转相互得到的是( )
A.△ACE和△BCD B.△ABF和△CFD C.△ABC和△CDE D.△AFH和△EDH
31. 如图,四边形ABCD中,AD=3,AB=4,BC=12,CD=13,
∠BAD=900,
(1)求证:BD⊥BC (2)计算四边形ABCD的面积(本题8分)
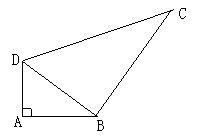
30.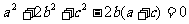 已知
已知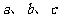 是△ABC的三边的长,且满足
,试判断此三角形的形状。(本题7分)
是△ABC的三边的长,且满足
,试判断此三角形的形状。(本题7分)
29、已知:a-b=2,b-c=3,c-d=4,
求:代数式(a-c) (b-d)÷ (a-d)的值。(本题7分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com