16．(6分)已知正比例函数的图象经过点(1，－2)，求此函数的解析式，并在坐标系中画出此函数的图象．

[解]设正比例函数解析式为y＝kx(k≠0)．

∵　 图象过(1，－2)，

∴ －2＝k．

∴　 函数解析式为y＝－2 x．

其图象如右图所示．

15．若直线y＝3 x+b 与两坐标轴所围成的三角形的面积为24，则b＝_________．

[提示]直线与y 轴交点坐标为(0，b)，与x 轴交点坐标为(－，0)，故

24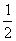＝·|b|·|－|．

[答案]±12．

[点评]根据直线与x 轴、y 轴交点坐标的求法．求面积时对含b 的式子要加绝对值符号．

14．如果二次函数y＝ax²+bx+c 的图象的顶点是(－2，4)，且过点(－3，0)，则a为_____________．

[提示]用顶点式求出二次函数解析式．

[答案]－4．

13．二次函数y＝－x²+mx+2的最大值是，则常数m＝_________．

[提示]可应用顶点坐标公式求出顶点纵坐标．

[答案]±1．

[点评]本题考查二次函数最大(小)值的求法．本题还可用配方法求解．

12．已知一次函数y＝kx+b(k≠0)，当x＝1时，y＝3；当x＝0时，y＝2．则函数解析式为________，函数不经过第_____象限，y 随x 增大而________．

[提示]设一次函数为y＝kx+b，把已知值代入求出k，b．

[答案]y＝x+2，四，增大．

[点评]本题考查一次函数的性质与解析式的求法．

11．当m＝_________时，函数(m²－m)是一次函数．

[提示]2 m²－m＝1，解得m₁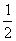＝－，m₂＝1(舍去)．

[答案]m＝－．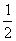

[点评]根据一次函数的定义，得2 m²－m＝1，且m²－m≠0．

10．若反比例函数的图象过点(－1，2)，则它的解析式为__________．

[提示]设反比例函数解析式为y＝，则k＝－2．

[答案]y＝－．

9．函数y＝中自变量x 的取值范围是___________．

[提示]由题意，得x－1≠0，x－3≠0．

[答案]x≠1，且x≠3．

[点评]注意零指数的底数不为0以及结论中的“且”字．

8．若二次函数y＝2 x²－2 mx+2 m²－2的图象的顶点在x 轴上，则m 的值是(　　 )

(A)0　　 (B)±1　　 (C)±2　　　 (D)±

[提示]由题意知D ＝0，即4 m²－8 m²+8＝0，故m＝±．

[答案]D．

[点评]抛物线的顶点在x 轴上，表明抛物线与x 轴只有一个交点，此时 D ＝0．

7．二次函数式y＝x²－2 x+3配方后，结果正确的是………………………………(　　 )

(A)y＝(x+1)²－2　　　 (B)y＝(x－1)²+2

(C)y＝(x+2)²+3　　　 (D)y＝(x－1)²+4

[提示]y＝x²－2 x+3＝x²－2 x+1+2＝(x－1)²+2．

[答案]B．