5．圆内接四边形ABCD中，∠A、∠B、∠C的度数比是2︰3︰6，则∠D的度数是(　　 )

(A)67.5°　　 (B)135°　　 (C)112.5°　　 (D)110°

[提示]因为圆内接四边形的对角之和为180°，则∠A+∠C＝∠B+∠D＝180°．又因为∠A︰∠B︰∠C＝2︰3︰6，所以∠B︰∠D＝3︰5，所以∠D的度数为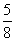×180°＝112.5°．[答案]C．

4．如图，已知⊙O的弦AB、CD相交于点E，的度数为60°，的度数为100°，则∠AEC等于………………………………………………………………………(　　 )

(A)60°　　 (B)100°　 (C)80°　 (D)130°

[提示]连结BC，则∠AEC＝∠B+∠C＝×60°+×100°＝80°．

[答案]C．

3．如图，在两半径不同的同心圆中，∠AOB＝∠A′OB′＝60°，则………………(　　 )

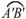(A)＝(B)＞

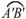
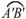(C)的度数＝的度数

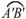(D)的长度＝的长度

[提示]因为在圆中，圆心角的度数与它所对的弧的度数相等，

而∠AOB＝∠A′OB′，所以的度数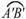＝的度数．[答案]C．

2．下列判断中正确的是………………………………………………………………(　　 )

(A)平分弦的直线垂直于弦(B)平分弦的直线也必平分弦所对的两条弧

(C)弦的垂直平分线必平分弦所对的两条弧(D)平分一条弧的直线必平分这条弧所对的弦

[提示]弦的垂直平分线平分弦、垂直于弦，因此平分弦所对的两条弧．[答案]C．

1．有下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧．其中正确的有………………(　　 )

(A)4个　 (B)3个　　 (C)2个　　 (D)1个

[提示]若三点在一条直线上，则不能作出过这三点的圆，故②不对．[答案]B．

[点评]本题考查直径、过不在同一条直线上的三点的圆、外心、等圆与等弧等概念，其中第②个命题不对的原因在于忽视了过三点作图的条件．

26．已知：如图，在四边形ABCD中，E为AB上一点，△ADE和△BCE都是等边三

角形，AB、BC、CD、DA的中点分别为P、Q、M、N，试判断四边形PQMN为怎样的四边形，并证明你的结论．

[提示]连结AC和CD，首先利用中位线定理和平行四边形判定定理，证明四边形PQMN为平行四边形，然后证明△AEC≌△DEB，得到AC＝BD，再证明□PQMN为菱形．

[答案]四边形PQMN为菱形．证明如下：

如图，连结AC、BD．

∵　 PQ为△ABC的中位线，

∴　 PQ 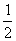AC．

同理　 MN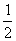AC．

∴　 MNPQ，

∴　 四边形PQMN为平行四边形．

在△AEC和△DEB中，

AE＝DE，EC＝EB，∠AED＝60°＝∠CEB，

即　 ∠AEC＝∠DEB．

∴　 △AEC≌△DEB．

∴　 AC＝BD．

∴　 PQ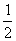＝AC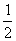＝BD＝PN．

∴　 □PQMN为菱形．

25．如图，在正方形ABCD中，点E、F分别在BC、CD上移动，但A到EF的距离

AH始终保持与AB长相等，问在E、F移动过程中：

(1)∠EAF的大小是否有变化？请说明理由．

(2)△ECF的周长是否有变化？请说明理由．

[提示]证明△EAH≌△EAB，△FAH≌△FAD．

[答案](1)∠EAF始终等于45°．证明如下：

在△EAH和△EAB中，

∵　 AH⊥EF，∴　 ∠AHE＝90°＝∠B．

又　 AH＝AB，AE＝AE，∴　 Rt△EAH≌Rt△EAB．

∴　 ∠EAH＝∠EAB．

同理　 ∠HAF＝∠DAF．∴　 ∠EAF＝∠EAH+∠FAH

＝∠EAB+∠FAD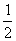＝∠BAD＝45°．

因此，当EF在移动过程中，∠EAF始终为45°角．

(2)△ECF的周长不变．证明如下：

∵　 △EAH≌△EAB，

∴　 EH＝EB．

同理　 FH＝FD．

∴　 △ECF周长＝EC+CF+EH+HF

＝EC+CF+BE+DF

＝BC+CD＝定长．

24．如图，在梯形ABCD中，AD∥BC，AB＝DC，BD⊥DC于D，且∠C＝60°，若

AD＝5 cm，求梯形的腰长．

[提示]求出∠CBD，∠ABD和∠ADC的度数，证明AB＝AD，或者过D点作DE⊥BC于E，CE为下底与上底的差的一半，又是CD的一半，CD又是BC的一半．从中找出CD与AD的关系．

[解法一]∵　 BD⊥CD，∠C＝60°，

∴　 ∠CBD＝30°．

在等腰梯形ABCD中，∠ABC＝∠C＝60°，

∴　 ∠ABD＝∠CBD＝30°．

∵　 AD∥BC，

∴　 ∠ADB＝∠CBD．

∴　 ∠ABD＝∠ADB．

∴　 AB＝AD＝5(cm)．

[解法二]过D点作DE⊥BC，垂足为E点．

∵　 在Rt△CDE中，∠CDE＝30°，

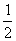∴　 CE＝CD．

又　 CE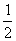＝(BC－AD)，

∴　 CD＝BC－AD．

即　 BC＝CD+AD．

又 在Rt△BCD中，∠CBD＝30°，

∴　 CD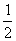＝BC．

∴　 CD＝2 CD－AD．

即　 CD＝AD＝5(cm)．

23．已知：如图，在□ABCD中，BE、CE分别平分∠ABC、∠BCD，E在AD上，

BE＝12 cm，CE＝5 cm．求□ABCD的周长和面积．

[提示]证明BE⊥EC和E为AD中点．

[答案]在□ABCD中，

∵　 AB∥CD，

∴　 ∠ABC+∠BCD＝180°．

∵　 ∠ABE＝∠EBC，∠BCE＝∠ECD，

∴　 ∠EBC+∠BCE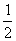＝(∠ABC+∠BCD)＝90°．

∴　 ∠BEC＝90°．

∴　 BC²＝BE²+CE²＝12²+5²＝13²．

∴　 BC＝13．

∵　 AD∥BC，

∴　 ∠AEB＝∠EBC．

∴　 ∠AEB＝∠ABE．

∴　 AB＝AE．

同理　 CD＝ED．

∵　 AB＝CD，

∴ 　AB＝AE＝CD＝ED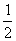＝BC＝6.5．

∴　 □ABCD的周长＝2(AB+BC)＝2(6．5+13)＝39．

　 S_□ABCD＝2 S_△BCE＝2·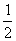BE·EC

＝12×5＝60．

22．证明等腰梯形判定定理：在同一底上的两个角相等的梯形是等腰梯形．(要求：画出

图形，写出已知、求证、证明．)

[提示]作辅助线，构造等腰三角形．

[答案]已知：在梯形ABCD中，AD∥BC，∠B＝∠C(图(1))．求证：AB＝DC．

[证法一]如图(1)，过点D作DE∥AB，交BC于E．

图(1)　　

∴　 ∠B＝∠1．又　 ∠B＝∠C，∴　 ∠C＝1．

∴　 DE＝DC．又　 AB∥DE，AD∥BE，

∴　 四边形ABED为平行四边形，∴　 AB＝DE．

∴　 AB＝DC．

[证法二]如图(2)，分别延长BA、CD，交于点E．

图(2)　

∵　 ∠B＝∠C，∴　 BE＝CE．

∵　 AD∥BC，∴　 ∠B＝∠1，∠C＝∠2．

∴　 ∠1＝∠2．∴　 AE＝DE．

∴　 BE－AE＝CE－DE，即AB＝DC．