12．如图，直线AB∥CD∥EF，则∠a+∠b－∠g＝　　 ．

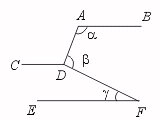
[提示]∵　AB∥CD，

∴　∠ADC＝∠a．

∵　∠ACD+∠CDF+∠b＝360°，

∴　∠a+∠b +∠CDF＝360°．

∴　∠a+∠b ＝360°－∠CDF．

∵　CD∥EF，

∴　∠CDF+∠g＝180°．

∴　∠a+∠b－∠g ＝360°－∠CDF－∠g ＝360°－(∠CDF+∠g)．

∴　∠a+∠b－∠g ＝180°．

[答案]180°．

11．如图，∠1＝82°，∠2＝98°，∠3＝80°，则∠4＝　　 ．

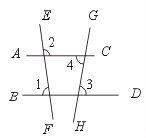
[提示]先判定AC∥BD．再利用平行线的性质求∠4的度数．

[答案]80°．

10．如图，AB∥CD、AF分别交AB、CD于A、C．CE平分∠DCF，∠1＝100°，则∠2＝　　　　 ．

[提示]先证∠DCF＝∠1＝100°，再用“角平分线家义”来求∠2．

[答案]50°．

9．如图，∠1的内错角是，它们是直线、被直线所截得的．

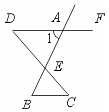
[答案]∠AEC和∠B，DF、DC(DF、BC)、AB．

8．如图，OA⊥OB，OC⊥OD．若∠AOD＝144°，则∠BOC＝______．

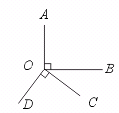
[提示]由OA⊥OB，OC⊥OD，可得∠AOB＝∠COD＝90°，一周角为360°．

[答案]36°．

7．如图，直线AB和CD相交于点O，OE是∠DOB的平分线，若∠AOC＝76°，则∠EOB＝_______．

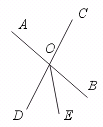
[提示]根据“对顶角相等”和“角平分线的定义”来求．

[答案]38°．

6．如图，直线AB、CD相交于点O，∠1＝∠2．则∠1的对顶角是_____，∠4的邻补角是______．∠2的补角是_________．

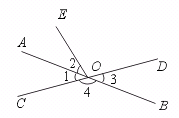
[提示]注意补角和邻补角的区别，前者只要求满足数量关系，即两角和为180°，而后者既要求满足数量关系又要求满足位置关系，即互补相邻．

[答案]∠1；∠1和∠3；∠BOE或∠4．

5．命题有真命题、假命题，定理也有真定理假定理…………………………………(　)

[提示]前一句话是对的，后一句话是错的．假命题不能成为定理，定理都是真命题．

[答案]×．

4．平面内两条不平行的线段必相交…………………………………………………(　)

[提示]仔细读题，想想线段的特征，线段有两个端点，有一定的长度，它们可以延长后相交，但本身可以既不平行，也不相交．

[答案]×．

[点评]平面内两条不平行的线段可以相交，也可以不相交，但平面内两条不平行的线段的延长线一定相交．

3．如果直线a⊥b，且b⊥c，那么a⊥c……………………………………………(　)

[提示]画图，a⊥b，则∠1＝90°，b⊥c，则∠2＝90°．

∴　∠1＝∠2．

∴　a∥c．

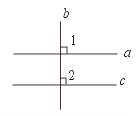
[答案]×．

[点评]由此题可知平面内垂直于同一直线的两直线互相平行，垂直关系没有传递性．