
5.如图,在Rt△ABC中,CD是斜边AB上的高,则图中的相似三角形共有………( )
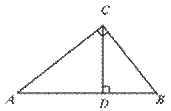
(A)1对 (B)2对 (C)3对 (D)4对
[提示]考虑Rt△ABC与Rt△ACD和Rt△CBD相似情况.
[答案]C.
[点评]本题要求运用直角三角形被斜边上的高所分割成两个直角三角形这种基本图形.
4.下列判断中,正确的是………………………………………………………………( )
(A)各有一个角是67°的两个等腰三角形相似
(B)邻边之比都为2︰1的两个等腰三角形相似
(C)各有一个角是45°的两个等腰三角形相似
(D)邻边之比都为2︰3的两个等腰三角形相似
[提示]设计出反例淘汰错误的选项.[答案]B.
[点评]本题要求运用相似三角形的判定定理.A不成立的原因是当底角为67°时,顶角为46°,另一个三角形的顶角为67°时,底角为66.5°,这两个等腰三角形不相似.C不成立的原因也是顶角不等.D不成立的原因是当一个等腰三角形的腰与底的比是2︰3时,另一个等腰三角形的腰与底的比为3︰2,它们三边之比分别为2︰2︰3与3︰3︰2.
3.如图,DE∥BC,在下列比例式中,不能成立的是………………………………( )
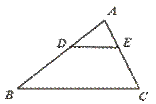
(A)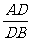 =
=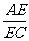 (B)
(B)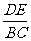 =
=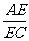 (C)
(C)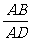 =
=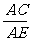 (D)
(D)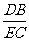 =
=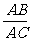
[提示]用特殊值法来筛选出选项,D、E分别为AB、AC的中点,计算每个线段比.[答案]B.
[点评]本题要求运用平行线分线段成比例定理和三角形一边平行线的性质定理,选B的原因是,当E为AC的中点时,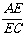 =1,D为AB的中点,
=1,D为AB的中点,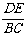 =
= .
.
2.已知线段d是线段a、b、c的第四比例项,其中a=2 cm,b=4 cm,c=5 cm,则d等于……( )
(A)1 cm(B)10 cm(C)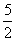 cm(D)
cm(D)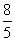 cm.
cm.
[提示]列出比例式:a︰b=c︰d,解出d.[答案]B.
[点评]本题要求运用比例的概念和求第四比例项的基本方法.
1.已知5y-4x=0,那么(x+y)︰(x-y)的值等于………………………………( )
(A)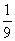 (B)-9 (C)9 (D)-
(B)-9 (C)9 (D)-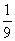
[提示]将5y-4x=0改写成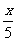 =
=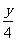 ,用比例性质得
,用比例性质得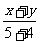 =
=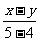 .[答案]C.
.[答案]C.
[点评]本题要求运用比例性质进行计算.
27.如图,如果D是BC的中点,那么B、C两点到直线AD的距离相等.试写出已知,求证,并补全图形(不证明).
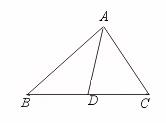
[提示]B、C两点的直线AD的距离,是点到直线的距离.即相应的“垂线段”的长度.可用三角尺画出图形.
[答案]图形如图所示,
已知:BD=CD,且BE⊥AD,CF⊥AD,垂足分别为E、F.
求证:BE=CF.
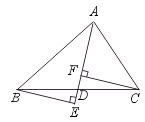
26.已知:如图,D是BC上的一点.DE∥AC,DF∥AB.
求证:∠A+∠B+∠C=180°.
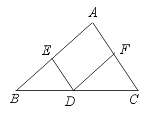
[提示]由DE∥AC,DF∥AB,先证:∠A=∠EDF,再证∠A+∠B+∠C=180°.
[证明]∵ DE∥AC(已知),
∴ ∠BED=∠A,∠BDE=∠C(两直线平行,同位角相等).
∵ DF∥AB(已知),
∴ ∠BED=∠EDF(两直线平行,内错角相等),
∠FDC=∠B(两直线平行,同位角相等).
∴ ∠EDF=∠A(等量代换).
∵ ∠BDE+∠EDF+∠FDC=180°(平角定义),
∴ ∠C+∠A+∠B=180°(等量代换).
即 ∠A+∠B+∠C=180°.
25.已知:如图,AD∥EF,∠1=∠2.求证:AB∥DG.

[提示]证明∠BAD=∠2.
[证明]∵ AD∥EF(已知),
∴ ∠1=∠BAD(两直线平行,同位角相等).
∵ ∠1=∠2(已知),
∴ ∠BAD=∠2(等量代换).
∴ AB∥DG(内错角相等,两直线平行).
24.如图,a∥b,c∥d,∠1=113°,求∠2、∠3的度数.
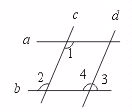
[提示]由a∥b,∠1=113°,可求∠2.由c∥d和求出的∠2的度数可求∠4.然而求出∠3.
[答案]∠2=113°.∠3=67°.
∵ a∥b(已知).
∴ ∠2=∠1=113°(两直线平行,内错角相等).
∵ c∥d(已知).
∴ ∠4=∠2=113°(两直线平行,同位角相等).
∵ ∠3+∠4=180°(邻补角定义),
∴ ∠3=67°(等式性质).
23.如图,∠B=∠D,∠1=∠2.求证:AB∥CD.
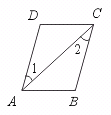
[证明]∵ ∠1=∠2(已知),
∴ ∥ ( ),
∴ ∠DAB+∠ =180°( ).
∵ ∠B=∠D(已知),
∴ ∠DAB+∠ =180°( ),
∴ AB∥CD( ).
[答案]AD,BC,内错角相等两直线平行;
B,两直线平行,同旁内角互补;
D,等量代换,
同旁内角互补,两直线平行.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com