15．如图，l₁∥l₂∥l₃，BC＝3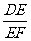，＝2，则AB＝___________．

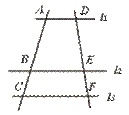
[提示]＝．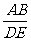

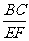[答案]6．

[点评]本题要求运用平行线分线段成比例定理．

14．已知数3、6，再写出一个数，使这三个数中的一个数是另外两个数的比例中项，这个数是___________(只需填写一个数)．

[提示]将b²＝ac中任意两个字母用3、6代替，求出第三个字母所表示的数．

[答案]±12或±3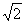或±．

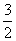[点评]本题要求运用比例的有关概念．它是一道开放性问题，用数3、5、6代替不同字母，答数也就不同．

13．如果x︰y︰z＝1︰3︰5，那么＝___________．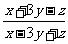

[提示]取x＝1，y＝3，z＝5代入，或设x＝k，则y＝3k，z＝5k．

[答案]－．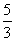

[点评]本题要求运用比例性质求值．

12．如图，将△ABC的高AD四等分，过每一个分点作底边的平行线，把三角形的面积分成四部分S₁、S_2、S₃、S₄，则S₁︰S_2︰S₃︰S₄等于……………………………(　)

(A)1︰2︰3︰4　(B)2︰3︰4︰5　(C)1︰3︰5︰7　(D)3︰5︰7︰9

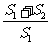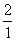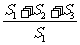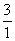[提示]＝()²，＝()²．

[答案]C．

[点评]本题要求运用相似三角形的面积比等于相似比的平方(即对应边上的高的比的平方)．

11．如图，点A₁、A₂，B₁、B₂，C₁、C₂分别是△ABC的边BC、CA、AB的三等分点，且ABC的周长为l，则六边形A₁A₂B₁B₂C₁C₂的周长为…………………………(　)

(A)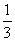l　　(B)3l　　(C)2l　　(D)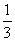l

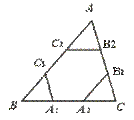
[提示]C₁B₂＝A₁A₂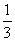＝BC，B₁A₂＝C₁C₂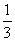＝AB，A₁C₂＝B₁B₂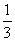＝AC．[答案]D．

[点评]本题要求运用相似三角形的周长比等于相似比(即　对应边的比)．

10．如图，在Rt△ABC中，∠C＝90°，CD⊥AB于D，且AD︰BD＝9︰4，则

AC︰BC的值为………………………………………………………………(　)

(A)9︰4　　(B)9︰2　　(C)3︰4　　(D)3︰2

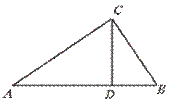
[提示]先设AD＝9k，BD＝4k，求出CD或AB，再求出AC和BC．[答案]D．

[点评]本题要求运用直角三角形被斜边上的高分成两个三角形与原三角形相似的定理．也可利用射影定理，由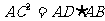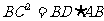，，得．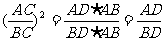

9．如图，D是△ABC的边AB上一点，在条件(1)∠ACD＝∠B，(2)AC²＝AD·AB，(3)AB边上与点C距离相等的点D有两个，(4)∠B＝∠ACB中，一定使

△ABC∽△ACD的个数是………………………………………………………(　)

(A)1　　(B)2　　(C)3　　(D)4

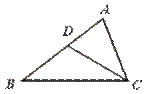
[提示]由于∠A为公共角，所以考虑另一个对应角相等或∠A的两边对应成比例，才能有△ABC∽△ACD．[答案]B．

[点评]本题要求运用相似三角形的判定定理．题中条件(4)，∠B与∠ACB都不是

△ACD的内角，不可能成为△ABC和△ACD的对应角．由下图可见，条件(3)不一定能使△ABC∽△ACD．

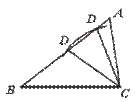
8．如图，在△ABC中，D为AC边上一点，∠DBC＝∠A，BC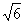＝，AC＝3，则CD的长为…………………………………………………(　)

(A)1　　(B)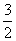　　(C)2　　(D)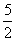

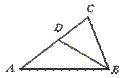
[提示]由△ABC∽△BDC，列出对应边的比例式．[答案]C．

[点评]本题要求运用相似三角形的判定定理与性质定理．

7．如图，□ABCD中，E是AD延长线上一点，BE交AC于点F，交DC于点G，则下列结论中错误的是…………………………………………………………………(　)

(A)△ABE∽△DGE　　(B)△CGB∽△DGE

(C)△BCF∽△EAF　　(D)△ACD∽△GCF

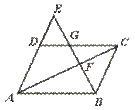
[提示]考察两个三角形中是否有对应边互相平行．[答案]D．

[点评]本题要求运用三角形相似的基本定理．

6．已知：如图，∠ADE＝∠ACD＝∠ABC，图中相似三角形共有………………(　)

(A)1对　　 (B)2对　(C)3对　　 (D)4对

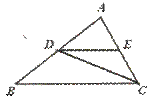
[提示]分别把CD、DE擦去，考察△ADE和△ABC、△ACD和△ABC的关系．[答案]C．

[点评]本题要求运用三角形相似的基本定理与判定定理的运用．